La geometría y su orígen
La geometría, del griego geo, "tierra" y methria, "medida", es una de las ramas más antiguas de las matemáticas y describe las formas de los objetos individuales, sus relaciones, las relaciones espaciales entre ellos y las propiedades de los objetos. se dedica al estudio del espacio que los rodea.
Inicialmente, el campo, como sugiere el nombre, siguió la medición en el sentido más práctico, pero con el tiempo la humanidad se dio cuenta de que incluso los símbolos y abstracciones más complejos pueden expresarse en términos geométricos. Surgieron así varias de sus ramas, junto con el análisis matemático y otras formas de computación, especialmente aquellas que combinan representaciones geométricas con fórmulas numéricas y algebraicas.
La geometría es una rama fundamental de las matemáticas que hace uso de muchas disciplinas (como la ingeniería y el dibujo arquitectónico) y sirve de complemento a muchas otras disciplinas como el diseño gráfico, física, mecánica, astronomía, literatura, etc. Además se empleó en la producción de muchos objetos hechos por el hombre, desde brújulas y fotocopiadoras hasta sistemas de posicionamiento global (GPS).
Tiene orígenes prácticos en las primeras civilizaciones humanas. Los antiguos babilonios fueron los inventores de la rueda y también inventaron la forma de la circunferencia. Por ello, probablemente fueron los primeros en reconocer las infinitas posibilidades del estudio de la geometría, y pronto la aplicaron a la astronomía. A partir de ellos podemos hacer una recopilación de las diversas culturas y sus aportaciones a está rama de las matemáticas.

Linea del tiempo
-
Grecia
s. VII a.C. - s. I a.C. aprox
Los griegos, conocedores de la geometría práctica egipcia, ampliaron este conocimiento sentaron las bases, con sus investigaciones y teorías, de la geometría que se utilizará durante siglos.
Operaban con números enteros, raíces cuadradas, fracciones, ecuaciones de primer y segundo grado, utilizaban números irracionales, resolvían problemas sobre la cuadratura del círculo, la trisección de un ángulo, las secciones cónicas y calcularon el número π.
Destacan entre los sabios griegos:
Tales de Mileto. Calculó la altura de la pirámide a partir de la sombra proyectada. Se le atribuyen varios teoremas; el de la suma de los ángulos de un triángulo y el de las paralelas.
Hipócrates. Conocía la relación entre los ángulos inscritos y arcos, la circunferencia circunscrita a un triángulo y su circuncentro.
Apolonio de Pérgamo. Sistematizó las secciones cónicas.
Pitágoras. Definió su famoso teorema (a2 = b2 + c2) e investiga sobre los poliedros que después difundirá Platón.
Platón. Consiguió dividir una circunferencia en cuatro partes iguales mediante dos diámetros perpendiculares cuyas diagonales formaban ángulos rectos.
Euclides. Escribió trece libros donde registró los avances en materia hasta su época.
-
Roma
753 a.C. - 476 d.C
El arquitecto más destacado fue Vitruvio, quién mencionó por primera vez en la historia la importancia de la relación entre el viento y la geometría en la planificación de una ciudad.
-
Mundo árabe
s. VII - XVIII
El imperio árabe tradujo a su idioma los restos de las obras griegas y romanas, y las recuperó tras siglos de olvido. Destacaron dos sabios que trabajaron sobre los conceptos de geometría no euclidiana, Omar Khayyam y Nasir Edin.
-
Renacimiento
s. XV - XVI
Comenzó a definirse en Italia, y especialmente en Florencia, un procedimiento para la representación gráfica conocida como perspectiva artificialis, la materialización de la visión humana en un soporte plano.
Artistas como Giotto, Van Eyck, Brunelleschi, Leon Batista Alberti, Paolo Ucello, Leonardo da Vinci, etc. trabajaron y perfeccionaron los fundamentos de la perspectiva.
Durero. Editó un texto para artistas, artesanos e ingenieros que tituló Enseñanza de la medida con regla y compás, era un geómetra nato que trazó los fundamentos de la antropometría, también escribió sobre el canon de la belleza humana.
Da Vinci. Dejó escrito en sus cuadernos que todos los problemas de perspectiva quedan aclarados por los cinco términos de las matemáticas, que son: el punto, la línea, el ángulo, la superficie y el sólido. Problemas que él mismo plantea en algunas de sus obras al hablar de diseños de algunas de sus iglesias, donde los polígonos regulares constituyen parte fundamental del diseño.
Regiomontano. Establece el desarrollo y solución sobre problemas de triángulos planos y esféricos, avances seguidos por Vieta, creador de la goniometría, en su búsqueda de la exactitud en un intento por cuadrar el círculo.
-
s. XVII
Nace la geometría análitica con Descartes y Fermat.
Descartes. Estudia en tres volúmenes las ecuaciones cuadráticas, curvas de distintos órdenes y la interrelación entre el álgebra y la geometría con ayuda de un sistema de coordenadas.
Fermat. Introdujo las coordenadas rectangulares y la aplicación de la geometría de los métodos algebráicos.
Newton. Trabajó sobre un sistema de coordenadas que denominó cartesiano. Clasificó las curvas según el número posible de puntos de intersección con la recta, obteniendo un total de setenta y dos tipos de curvas.
-
s. XVIII
El siglo de la consolidación de las diversas geometrías: la analítica, la diferencial, la descriptiva y la proyectiva.
Geometría analítica. es la parte de la geometría que estudia las figuras y transformaciones geométricas dadas por las ecuaciones algebraicas.
Eulesm sistematizó la geometría analítica estudiando en plano, y se interesó también por las transformaciones de los sistemas de coordenadas, las curvas según el grado de ecuaciones, las secciones cónicas, las tangencias, etc. Otros investigadores en geometría analítica son Gaspar Monge y Mener.
Geometría diferencial. estudia los objetos geométricos, las curvas y las superficies por medio del cálculo diferencial. Euler introdujo el concepto de superficie desarrollable.
Geometría descriptiva y proyectiva. fue Gaspar Monge quién aclaró el método y objeto de la descriptiva desarrollando los planos tangentes, normales a superficies curvas, la intersección de superficies curvas y las curvaturas de líneas y superficies.
-
s. XIX
Poncelet es quien culmina los estudios de Monge, Desargues y Pascal sobre la geometría proyectiva. También el ruso Lobachevsky investigó sobre la geometría no euclidiana. Otros investigadores destacados son: Karl Georg Christian von Staudt, Arthur Cayley, Luigi Cremona, August F. Möbius y Julius Plücker.
Objeto estudio
Según el diccionario de la lengua española, geometría es una palabra procedente del griego (medida de la tierra), que significa:
- Estudio de las propiedades y de las medidas de las figuras del plano o del espacio.
- Aplicación del álgebra a la geometría para resolver, por medio del cálculo, ciertos problemas de la extensión.
- Estudio de figuras que utiliza un sistema de coordenadas y los métodos de análisis matemático.
- Parte de la geometría que considera las figuras cuyos puntos no están todos en el plano.
- Parte de las matemáticas que tiene el objeto de resolver los problemas de la geometría del espacio por medio de las operaciones efectuadas en un plano y representar en él las figuras de los sólidos.
- Rama de la geometría que trata de la proyecciones de las figuras sobre el plano.
La geometría elemental se divide en dos partes, geometría plana (estudia las figuras planas, que tienen únicamente dos dimensiones: largo y ancho) y geometría del espacio (estudia las propiedades de los cuerpos geométricos provistos de largo, ancho y altura o profundidad).
Para comprender la geometría plana de manera mas clara, es indispensable, comenzar por la definición de conceptos elementales hasta llegar a nociones más complejas.
Indica una posición en el espacio, se designa con letra mayúscula.
Un punto señala una posición en el espacio. Conceptualmente no tiene largo, ancho, ni altura, por lo tanto, es estático, central y sin dirección.
Como elemento fundamental de la geometría, un punto puede determinar:
- los dos extremos de una línea
- la intersección de dos líneas
- el encuentro de líneas en la arista de un plano o un volúmen
- el centro de un campo

La prolongación de un punto, sucesión de puntos alineados sin principio ni final. Se designa con letra mayúscula, presenta tres características:
- longitud
- dirección
- posición
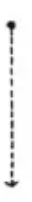
Hay dos subtipos:
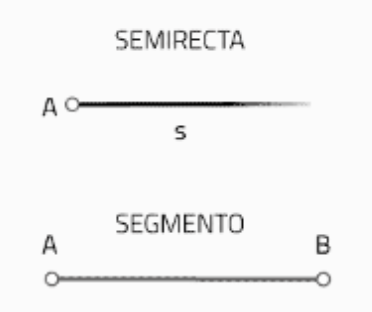
- Semirrecta. Cuando la recta tiene un origen concreto en un espacio y el otro extremo es infinito (impropio).
- Segmento. Cuando está limitada por ambos extremos por puntos.
La extensión de una línea, está formado por infinitas rectas y no tiene límites. Se designa con letra mayúscula, a menudo con el alfabeto griego. Presenta las siguientes características:
- longitud y anchura
- forma
- superficie
- orientación
- posición

La extensión de un plano, las características que lo conforman:
- longitud, anchura y profundidad
- forma y espacio
- superficie
- orientación
- posición
Geometría plana
Este campo de la geometría a menudo se ocupa de simplificar el mundo que nos rodea a un solo plano, por lo que no podemos explorar todas las características de un objeto. Por ejemplo, no es posible analizar todas las dimensiones de una caja, sino solo cada cara como un rectángulo.
La geometría plana tiene raíces antiguas, siendo su premisa principal Los Elementos del matemático griego Euclides, que datan del siglo IV a.C. Considerado uno de los textos más influyentes de la historia, resume conceptos básicos como líneas y polígonos, e incluso de encuentra el famoso teorema de Pitágoras.