Razón y proporción
En geometría debemos considerar los siguientes conceptos:
Conformidad, correspondencia y equilibrio de una de las partes con el todo o de cosas relacionadas entre sí.
Es la relación entre dos números o segmentos. Nos permite compararlos para saber cuántas veces uno contiene el otro.
La razón de dos segmentos a y b, se representa a/b = k, que se lee a es a b. La razón se denomina k.
Es la igualdad de dos razones. Se representa por a/b = c/d, que se lee a es a b como c es a d.
Directa e inversa
Al comparar dos segmentos, pueden ser iguales cuando al superponerlos coinciden, o diferentes cuyo caso nos puede indicar una relación de proporcionalidad. La igualdad es una proporción de la razón 1.
Son las que aumentan o disminuyen guardando la misma relación.
Dos segmentos a y b son directamente proporcionales si al multiplicar o dividir por n uno de ellos, también se ha de multiplicar o dividir por n el otro para mantener la misma razón.
Se puede expresar: a/b = c/d = … = k
a y b, c y d son parejas de segmentos directamente proporcionales.
Son aquellas en las que cuando una aumenta, la otra disminuye en la misma proporción. Esto se puede expresar diciendo que dos magnitudes son inversamente proporcionales cuando varían manteniendo su producto constante.
La proporción inversa puede representarse como:
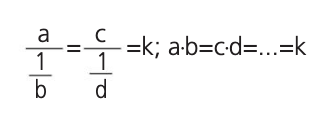
Donde a y b, c y d, son segmentos inversamente proporcionales.
Teorema de Tales
Se basa en la semejanza de triángulos, donde se afirma que esto ocurre solo sí se cumplen dos criterios: los ángulos que los componen iguales en ambos casos, y cada uno de sus lados son proporcionales. Es así como se establece la premisa que al dibujar una línea que sea paralela a uno de los lados de un triángulo, esto formará otro triángulo semejante al primero.
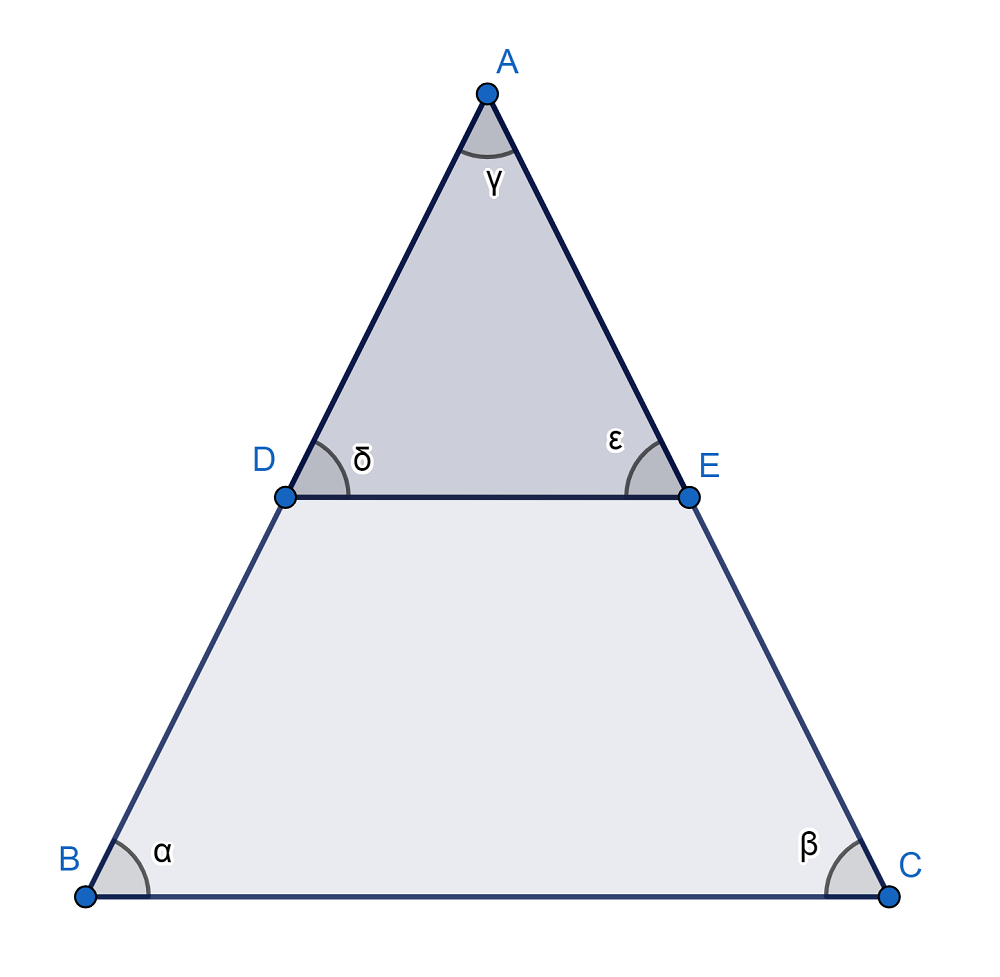
Por el teorema de Tales se puede concluir que α=δ y β=ε
Además, como mencionamos previamente, los lados son proporcionales, por lo que se cumple que:
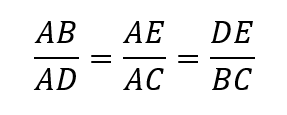
Historia del Teorema
Tales fue un filósofo griego de la tierra de Milatos, que sentía un gran interés por las matemáticas y responder interrogantes en torno al mundo físico. Esto lo llevó a viajar a Egipto para ampliar sus conocimientos; pero una vez en el lugar, se sintió inmensamente atraído hacia las monumentales pirámides de Guiza. Tan grande fue la impresión, que se mostró interesado en averiguar la altura de la Pirámide de Guiza.
Para responder esta interrogante, se basó en la semejanza de triángulos. Hizo su primera suposición, declarando de esta manera que los rayos del sol que entraban a la tierra eran perpendiculares. Identificó un triángulo, donde los catetos B y A hacían referencia a la longitud que se generaba desde el centro de la pirámide hasta el extremo de la sombra y la altura de la pirámide respectivamente; el valor de este último era desconocido. El segundo triángulo lo construye utilizando una vara, que pasa a conocerse como el cateto C y la sombra que este genera, siendo el cateto D. De esta manera se sabe que se trata de dos triángulos rectángulos.
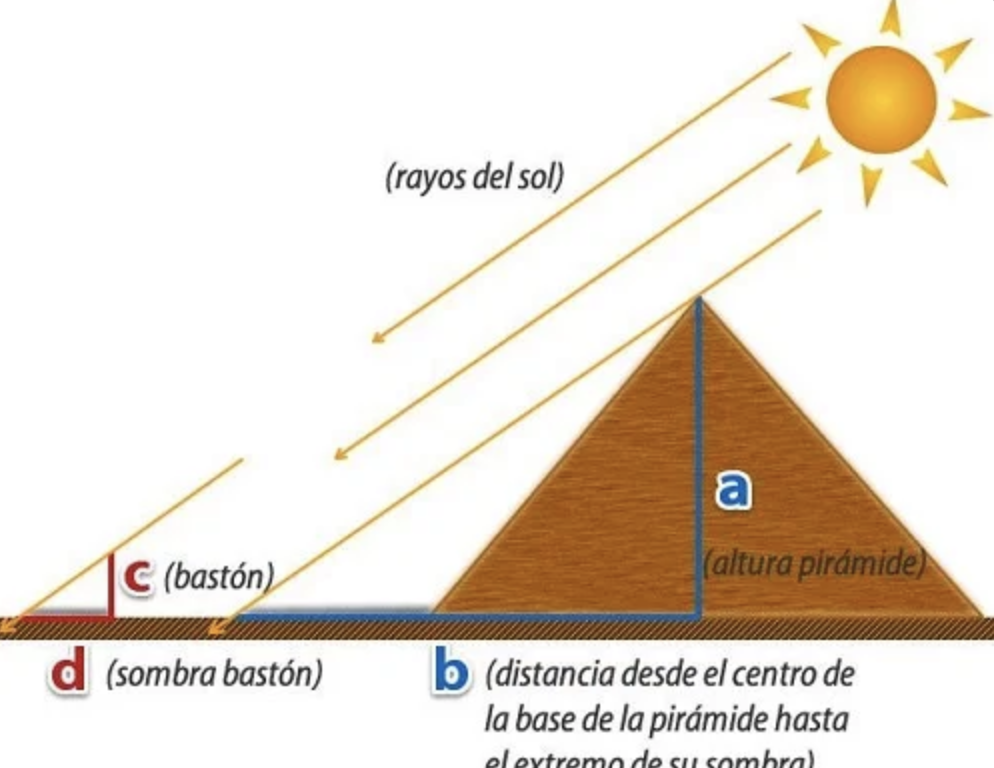
Ya establecidos estos factores, Tales realizaba mediciones en una hora determinada del día, justo en el momento en que la longitud de la sombra de la vara era igual al tamaño de la vara. De esta manera, afirmó que esto podía ser aplicado a la pirámide, declarando que en ese mismo momento del día, la sombra de esta debía tener la misma longitud que altura, pudiendo medir y determinar el valor de la altura del monumento.
Aplicación del teorema de Tales
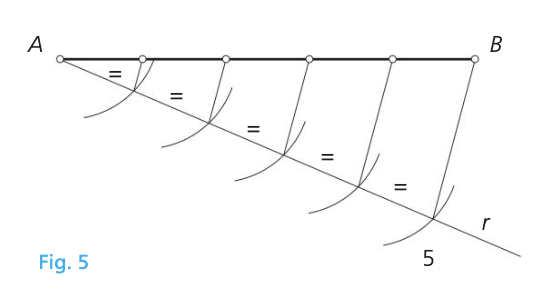
División de un segmento en partes iguales
- Se AB el segmento que se quiere dividir en n partes iguales.
- Se dibuja una semirrecta r de origen en uno de los extremos AB, por ejemplo, A.
- Se lleva sobre r, a partir de A, un número n de segmentos arbitrarios iguales.
- Uniendo el extremo del último, el 5 en este caso, con B y dibujando paralelas por los otros, se obtienen sobre AB los puntos que forman la división.