En geometría la línea se define como una sucesión de puntos o trayectoria de un punto en movimiento. La línea recta cuándo se tiene una dirección específica, pero consideramos línea curva cuando ninguna porción de ella es de forma recta.
Las curvas se clasifican en cónicas, cuando son origen de la sección de un plano y un cono, y curvas técnicas que están formadas por varios arcos de circunferencias tangentes entre sí, incluyen figuras como el óvalo, ovoide, espirales, envolventes y curvas cíclicas.
Curvas cónicas
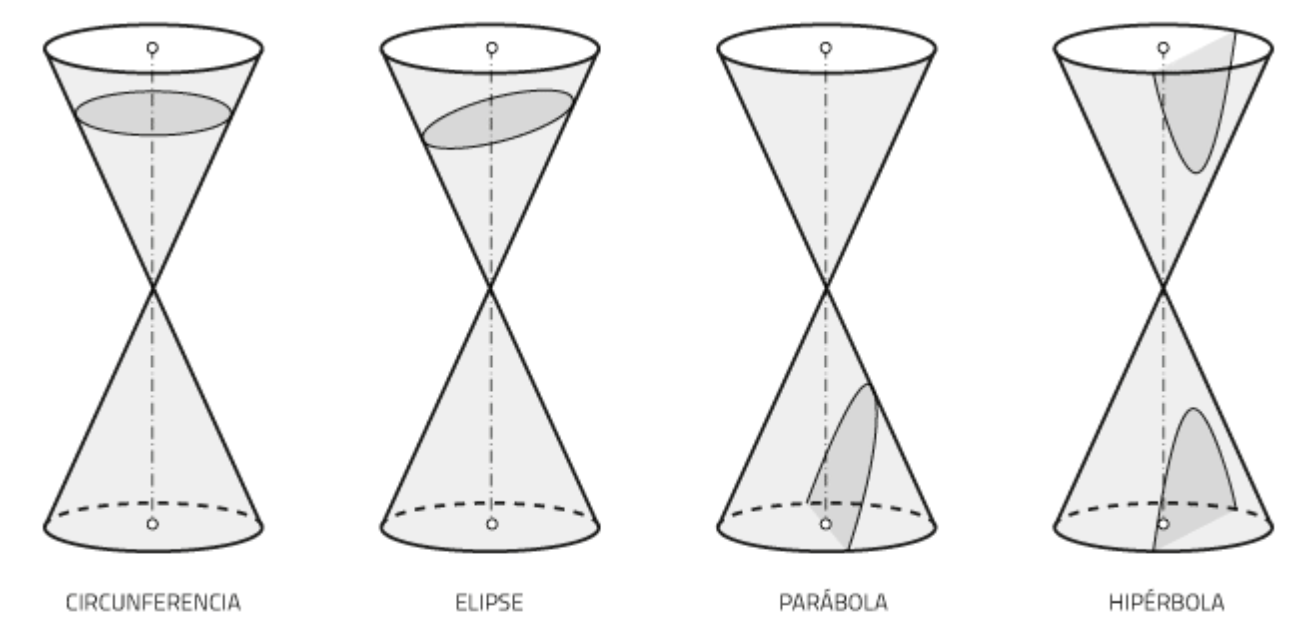
Se definen como secciones producidas por un plano secante en una superficie cónica de revolución (un cono), según la posición del plano y del cono podemos distinguir tres curvas importantes distintas; la parábola, la hipérbola y la elipse.
Tipos de curvas:
-
Elipse.
Es una curva cerrada plana
Lugar geométrico de los puntos del plano cuya suma de distancias a dos fijos denominados focos es constante. -
Parábola.
Es una curva plana, abierta y de una rama.
Lugar geométrico de los puntos del plano que equidistan de uno fijo denominado foco, y de una recta denominada directriz. -
Hipérbola.
Curva plana, abierta y con dos ramas.
Lugar geométrico de los puntos del plano cuya diferencia de distancias a otros dos fijos denominados focos es constante.
Construcción
Curvas técnicas
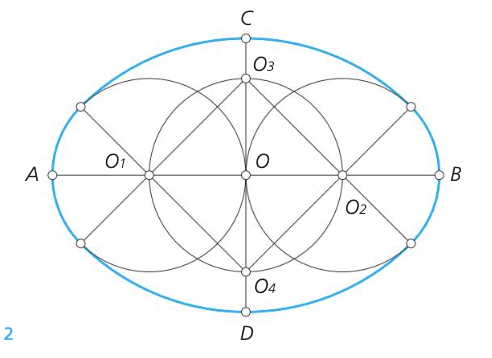
Es una curva cerrada y plana compuesta por un número par de arcos de circunferencia enlazados entre sí y simétricos respecto sus ejes mayor y menor normales entre sí.
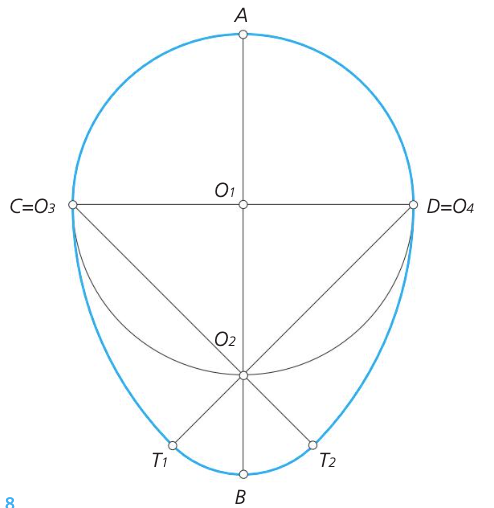
Es una curva cerrada y plana compuesta por dos arcos de circunferencia de igual radio, y otros dos de distinto radio, uno de ellos una semicircunferencia.
Tiene un eje de simetría que contiene a los centros de los arcos desiguales. Se denomina diámetro en el ovoide al diámetro de la semicircunferencia normal al eje.
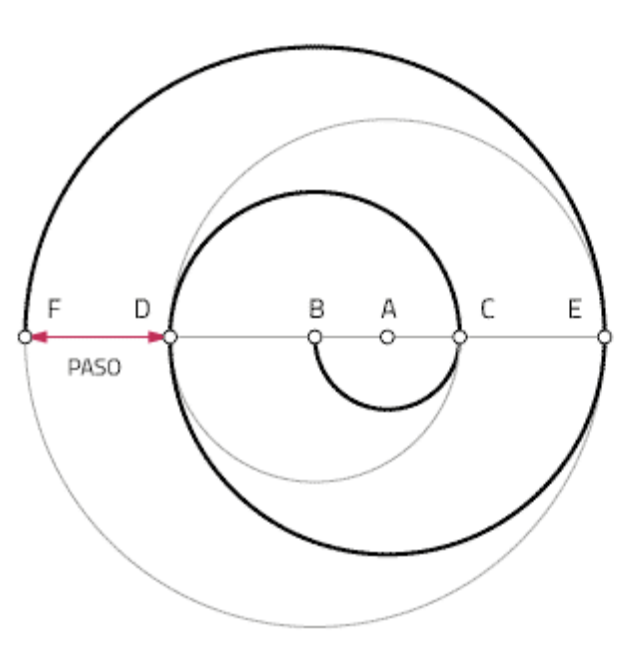
Curva abierta y plana generada por el movimiento de un punto que se aleja de otro u otros fijos denominados centros. Puede estar constituida por arcos de circunferencia enlazados entre sí y de radios gradualmente mayores.
Se denomina espira al fragmento de curva que describe el punto en una vuelta completa.
Las espiras contiguas distan entre sí una magnitud constante denominada paso.
Es una curva plana, en forma de espiral, formada por arcos de circunferencia tangentes entre sí, siendo los centrosde estos arcos los vértices del poligono inicial.
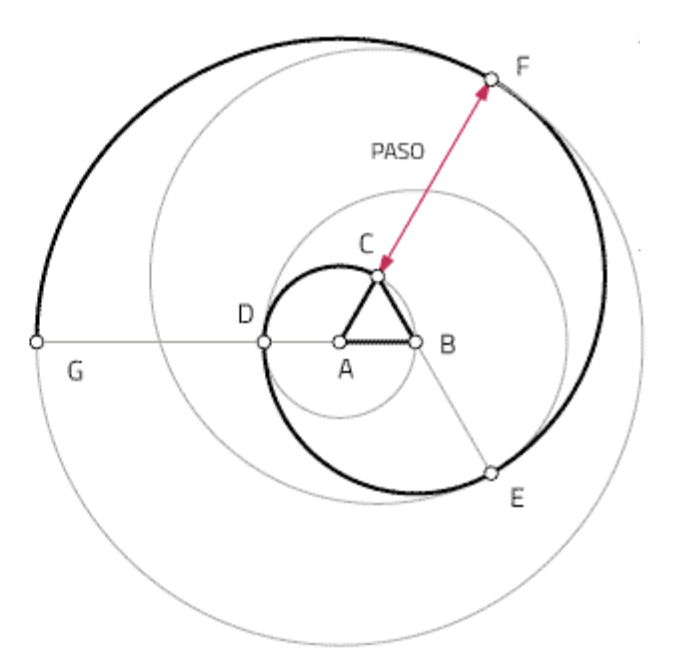
Construcción
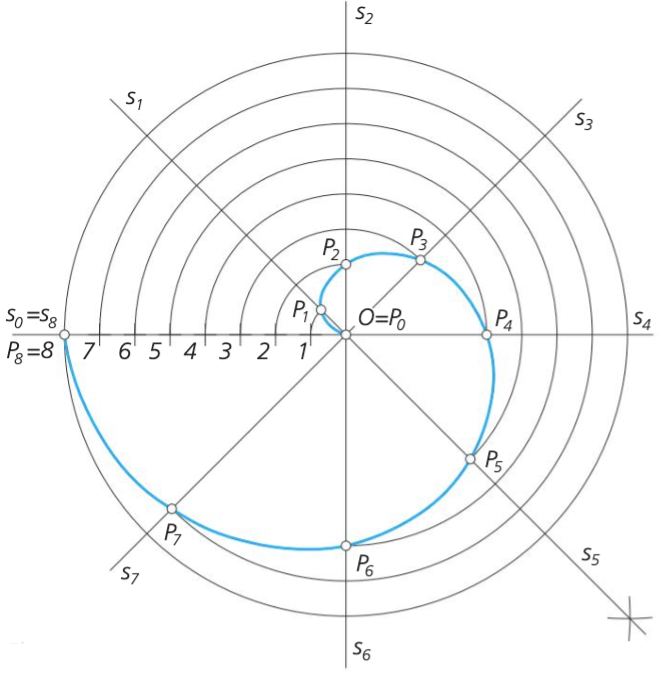
La espiral de Arquímedes
La espiral de Arquímedes o espiral aritmética es una curva que se aleja de un punto fijo (llamado centro) con una velocidad angular constante. Obtuvo su nombre del matemático griego Arquímedes, quien vivió en el siglo III antes de Cristo.
Técnicamente se define como el lugar geométrico de un punto moviéndose a velocidad constante sobre una recta que gira sobre un punto de origen fijo a velocidad angular constante.
Construcción
Curvas cíclicas
Son curvas planas, generadas por un punto perteneciente a una circunferencia que rueda (sin resbalar) sobre otra circunferencia o una recta. Se denominan cíclicas porque se repite su trazado.
Revisemos algunos ejemplos:
Es la curva plana que se obtiene mediante la trayectoria que describe un punto a(t) sobre una circunferencia que está rodando sin deslizarse de forma tangente sobre el exterior de una segunda circunferencia del mismo radio, siendo esta última fija. El nombre le viene de la forma de corazón que tiene la curva.
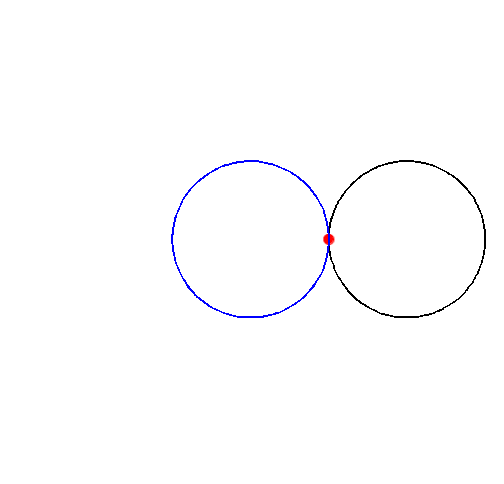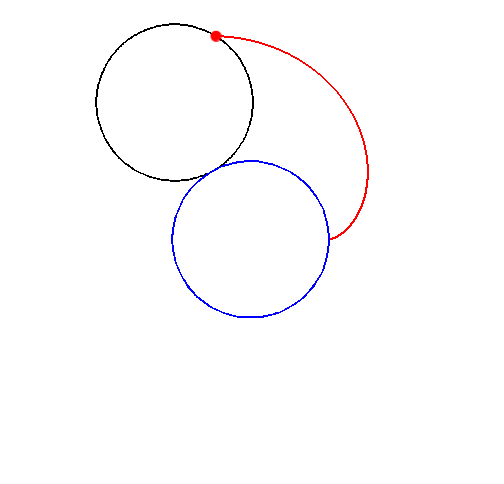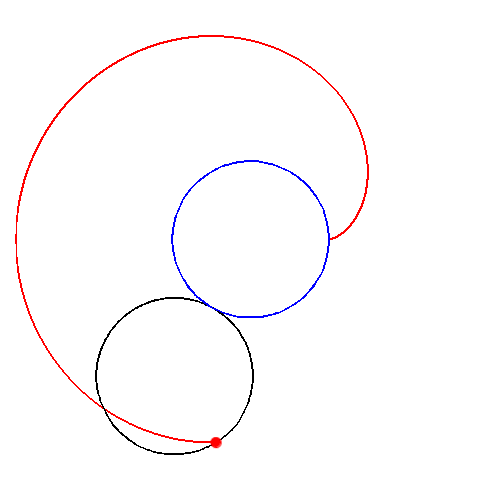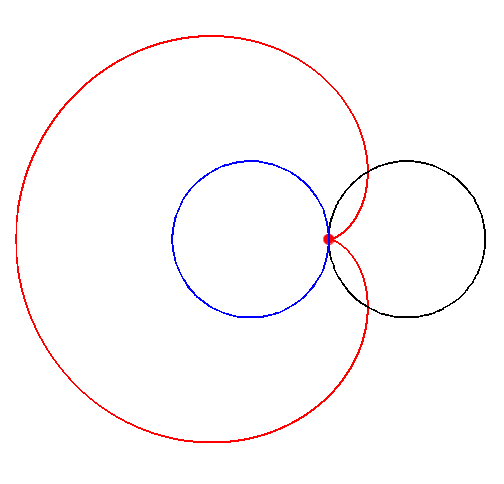
La nefroide es una epicicloide de dos puntos de retroceso cuya forma es la de un riñón. Es engendrada por una circunferencia de radio a que gira exteriormente sin deslizar sobre una circunferencia de radio 2a y de centro 0.
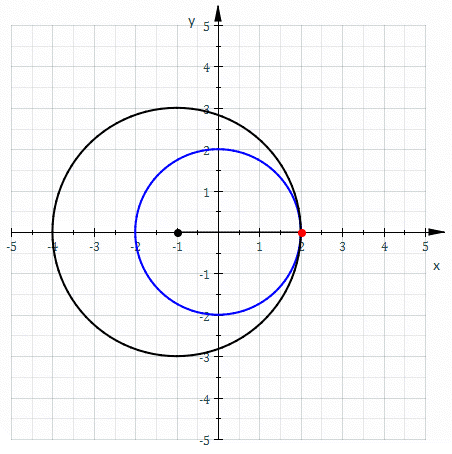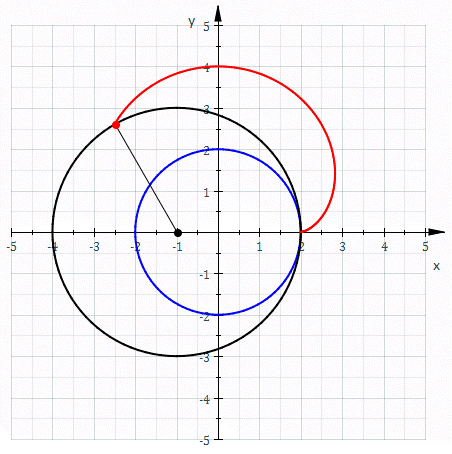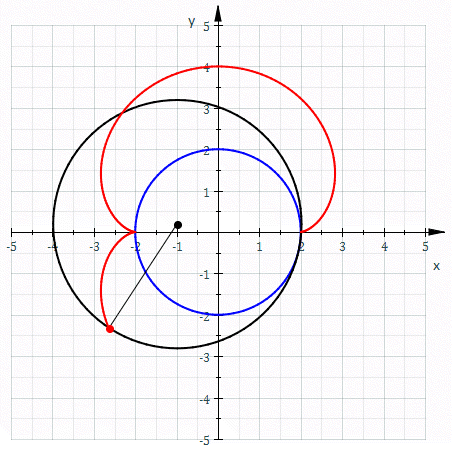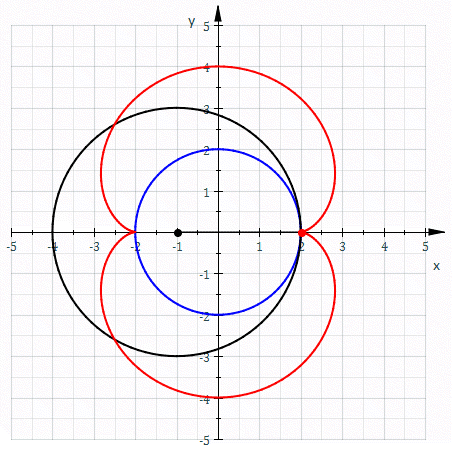
También conocida como tricuspídea o curva de Steiner, es una hipocicloide de tres cúspides. En otras palabras, es la ruleta creada por un punto del contorno de una circunferencia mientras rueda sin deslizar en el interior de un círculo con tres veces o una vez y media su radio. Su nombre se debe a su parecido con la letra griega delta.
De manera más general, una deltoide puede referirse a cualquier figura cerrada con tres vértices conectados por curvas que son cóncavas con respecto al exterior, lo que hace que los puntos interiores sean un conjunto no convexo.
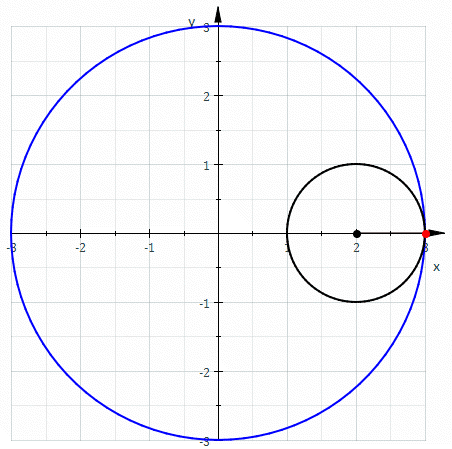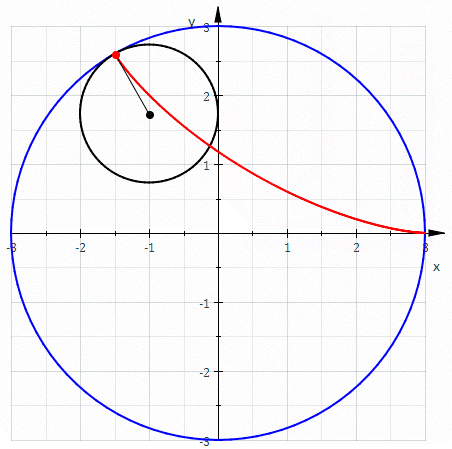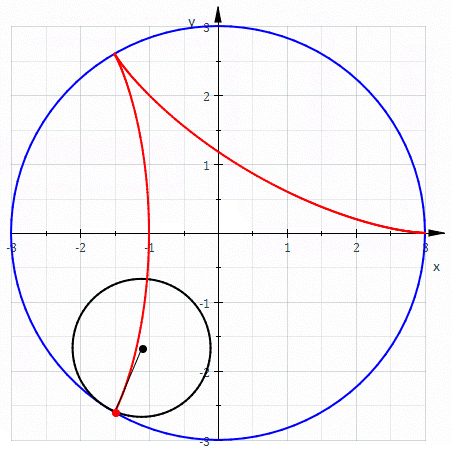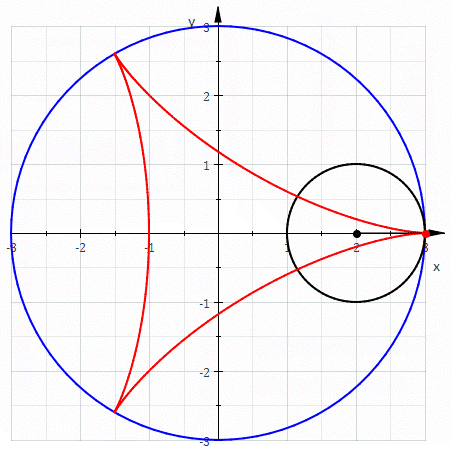
Construcción
FUENTES DE INFORMACIÓN
Colaboradores de Wikipedia. (23 diciembre 2022). Cardioide. Wikipedia, la enciclopedia libre. https://es.wikipedia.org/wiki/Cardioide
Colaboradores de Wikipedia. (11 diciembre 2019). Curva deltoide. Wikipedia, la enciclopedia libre. https://es.wikipedia.org/wiki/Curva_deltoide
Colaboradores de Wikipedia. (23 septiembre 2022). Nefroide. Wikipedia, la enciclopedia libre. https://es.wikipedia.org/wiki/Nefroide
Curvas cíclicas. (2020, 25 abril). Dibujo Técnico. https://dibujotecni.com/geometria-plana/curvas-ciclicas/
Curvas cónicas. Conceptos y tipos. Teorema de Dandelin. Directrices, excentricidad. (2020, 27 abril). Dibujo Técnico. https://dibujotecni.com/geometria-plana/curvas-conicas/
Óvalo, ovoide y espirales. (2021, 24 marzo). Dibujo Técnico. https://dibujotecni.com/geometria-plana/ovalo-ovoide-espirales/
Regato Abascal, G. et al (2019). Dibujo técnico I. Editex.