Antecedentes
Desde la antigüedad el hombre ha tratado de plasmar y representar de alguna forma la realidad, lo ha intentado no sólo con el lenguaje, transmitiendo su perspectiva en obras literarias, sino que ha tratado de hacerlo gráficamente. El hombre prehistórico lo hizo valiéndose de las pinturas rupestres, el hombre actual con obras abstractas, tratando de hacer complejas representaciones de la realidad.
En lo que respecta a esta síntesis introductora de los sistemas de representación axonométricos, no hablaremos de la representación a través del arte, aunque muchas obras sí emplean los sistemas de representación en su construcción, sino que hablaremos de los trazos y expresiones gráficas que nos dicen cómo está construida la realidad.
Para empezar, nos apoyaremos en la geometría descriptiva que tiene por objeto la representación de las figuras del espacio real en un plano bidimensional, se vale de la geometría proyectiva con el uso de medidas y técnicas que posibilitan la representación. La geometría descriptiva es la base de los distintos sistemas de representación.
Los sistemas de representación, como su nombre lo indica, cumplen el objetivo de representar volúmenes u objetos tridimensionales en un soporte bidimensional, en este caso la pantalla de tu computadora. ¡Veamos de que se trata!

Generalidades
Al igual que en el dibujo técnico, las representaciones gráficas se van a construir a partir de los tres sistemas de representación que ofrece la geometría descriptiva.
- Sistema diédrico, de doble proyección o de Monge
- Sistema axonométrico
- Sistema cónico o central
Estos sistemas tienen diversos métodos o formas de realizarse pueden ser por proyección, por coordenadas y localización de puntos, por abatimiento, etc. Pero es importante hacer la precisión de que independientemente de que método se realice el resultado será el mismo. Sin embargo, cambiar de sistema o subsistema si conduce a resultados diferentes.
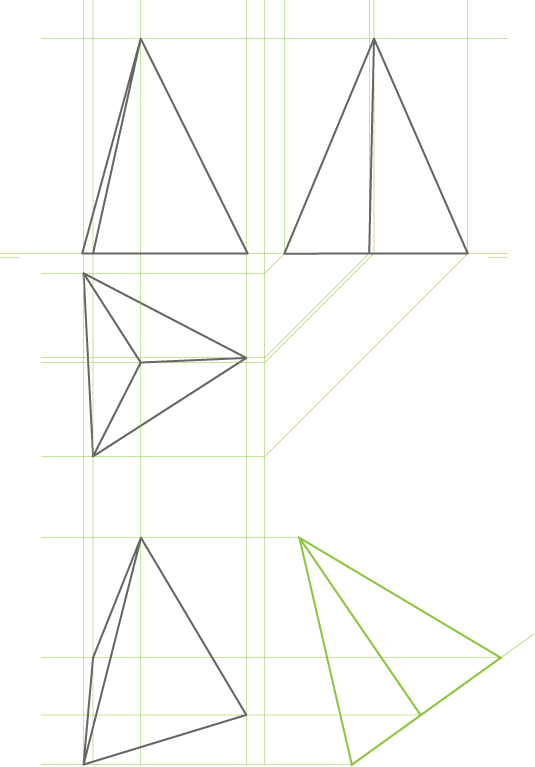
Estos sistemas tienen diversos métodos o formas de realizarse pueden ser por proyección, por coordenadas y localización de puntos, por abatimiento, etc. Pero es importante hacer la precisión de que independientemente de que método se realice el resultado será el mismo. Sin embargo, cambiar de sistema o subsistema si conduce a resultados diferentes.
- Sistema: conjunto ordenado de reglas, código proyectivo.
- Subsistema: variante de un sistema.
- Método: camino o forma de realizarse un sistema; invariante de un sistema o subsistema.
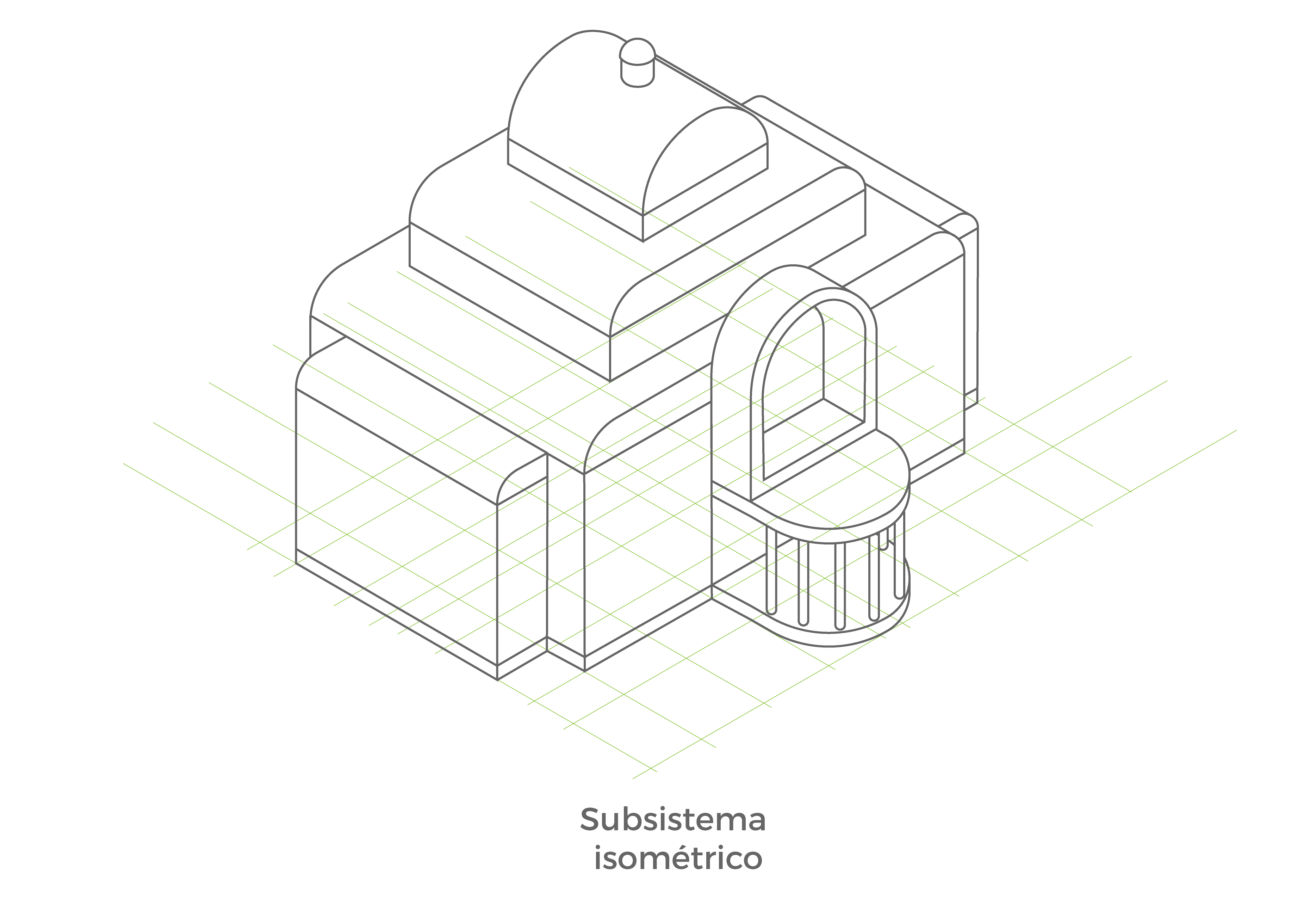
En el caso del ejemplo mostrado:
Sistema: Axonométrico.
Subsistema: Isométrico.
Método: Por proyección.
Tipos de proyección
Los sistemas y subsistemas de representación forman un complejo sistema de clasificación. Vamos a revisar primero cómo se clasifican de acuerdo con los rayos proyectantes, por lo que se pueden dividir en dos tipos principales de proyección:
- Proyección paralela o cilíndrica
- Proyección cónica o central
La proyección de los objetos sobre el plano de cuadro o de proyección se realiza mediante rayos proyectantes, líneas imaginarias que pasan por los vértices o puntos más notables del objeto que en su intersección con el plano del cuadro proyectan dicho vértice o punto.
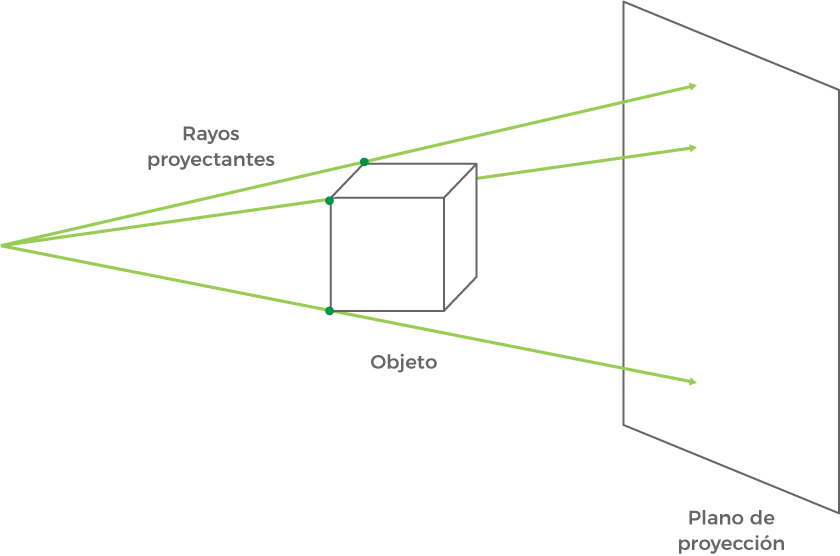
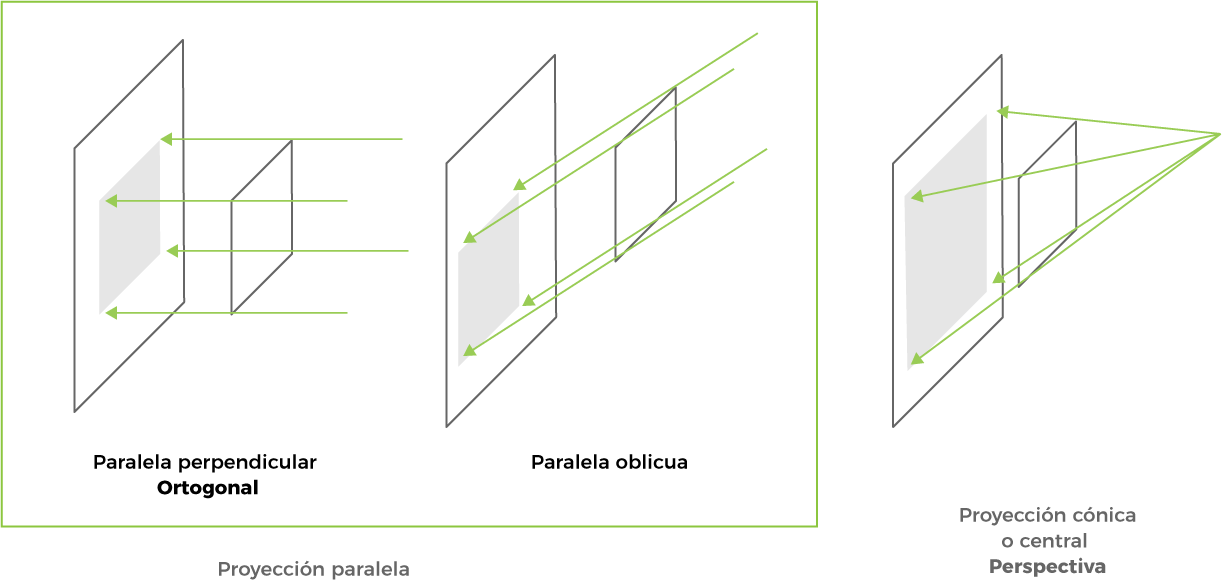
En la proyección paralela los rayos proyectantes parten de un punto en el infinito, lo que se denomina punto impropio y de acuerdo con su inclinación podemos clasificarlos en dos categorías:
- Proyección perpendicular u ortogonal: En este caso los rayos proyectantes son perpendiculares al plano geometral.
- Proyección oblicua: Los rayos proyectantes son paralelos, pero resultan oblicuos respecto al plano geometral.
En el caso de proyección cónica o central, como su nombre lo indica, los rayos proyectantes proceden de un punto central de proyección (punto propio), pasando por el objeto formando un haz cónico. Este tipo de perspectiva nos produce un aspecto global del volumen muy similar al que produce la retina humana, no profundizaremos en este sistema.
Veamos algunas de sus características:
- Los rayos de proyección paralelos intersectan perpendicularmente al plano del cuadro.
- Todas las distancias y superficies paralelas al plano del cuadro aparecen en verdadera magnitud.
- La magnitud de la figura es independiente de la distancia del objeto al plano del cuadro.
- A cada punto del espacio le corresponde un punto en la figura.
- Los rayos de proyección paralelos inciden oblicuamente desde arriba sobre el objeto y el plano del cuadro.
- La magnitud de la figura es independiente de la distancia del objeto al plano del cuadro.
- Las axonometrías que se encuentran en este tipo de proyección son rápidas y fáciles de construir; son de distancia infinita.
- Los rayos de proyección proceden de un punto central de proyección.
- La magnitud de la figura depende de la distancia del objeto al plano del cuadro.
- La figura corresponde a la impresión del ojo, con una diferencia.
- La superficie sobre la que se proyecta la figura en el ojo es curva mientras que en la perspectiva es plana, como en la fotografía.
Existe una relación compleja entre los sistemas de proyección, los subsistemas y los tipos de proyección. Para dejar esto más claro a continuación se muestra un esquema de clasificación.
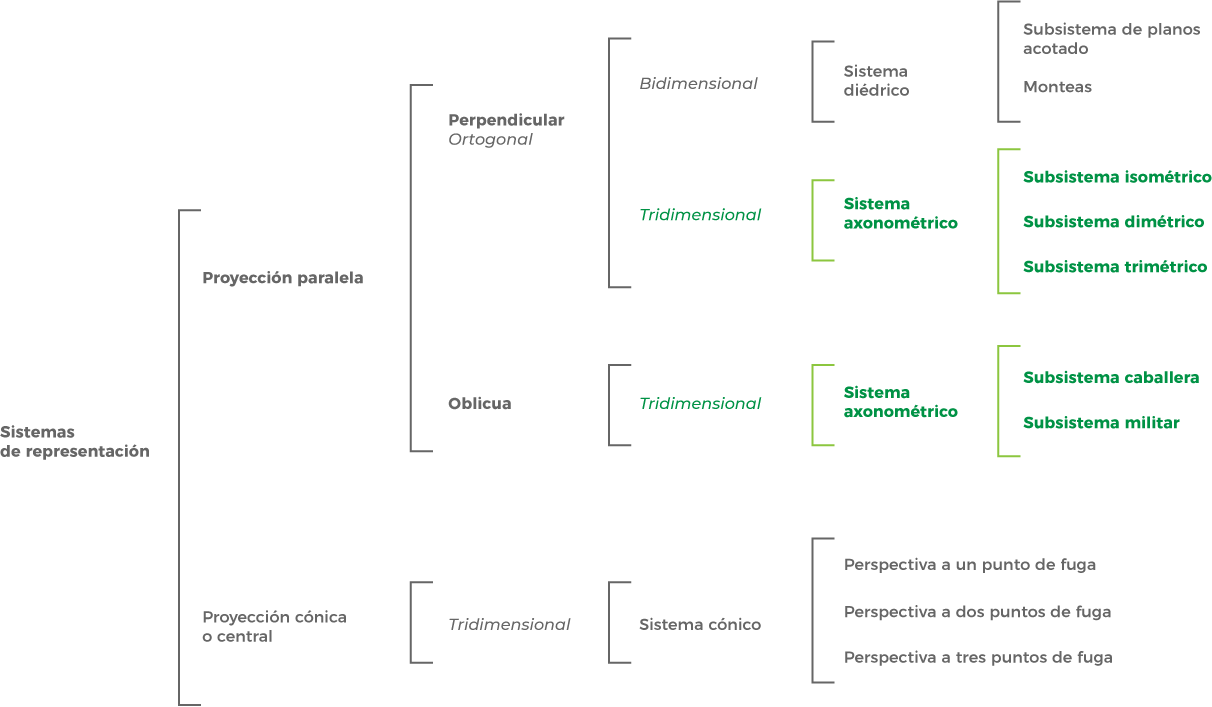
Características del sistema axónométrico
El sistema axonométrico nos proporciona una visión general de las dimensiones de los objetos con apariencia de perspectiva, este tipo de representación es muy útil para volúmenes en detalle, fragmentos de arquitectura, diseño de envases y exhibidores de mostrador, y en general para cualquier elemento de pequeño formato.
Se caracterizan por representar los objetos mediante una única proyección, pudiéndose apreciar en ella, de un solo golpe de vista, la forma y proporciones de los mismos. Tienen ventaja de que al tener ejes paralelos y perpendiculares, su desarrollo es de mayor facilidad que en la proyecciones cónicas, sobre todo cuando se cuanta con gran cantidad de curvas.
Aunque el objetivo de estos sistemas es representar los objetos como los vería un observador situado en una posición particular respecto al objeto, esto no se consigue totalmente, dado que la visión humana es binocular, por lo que a lo máximo que se ha llegado, concretamente, mediante la proyección cónica, es a representar los objetos como los vería un observador con un solo ojo.
La constricción de los diversos subsistimos axonométricos son de mayor facilidad que la proyección cónica, en sus constricción todos los trazos son paralelos y perpendiculares, lo que permite una construcción de volúmenes y sombras de manera más sencilla.
Para su construcción intervienen tres planos auxiliares, formando un triedro trirectángulo, que tiene su vértice O coincidente con el plano del cuadro.
El fundamento del sistema consiste en: proyectar los puntos y el volumen a representar ortogonalmente sobre estos planos auxiliares, para posteriormente proyectarlos, también ortogonalmente, sobre el plano del cuadro.
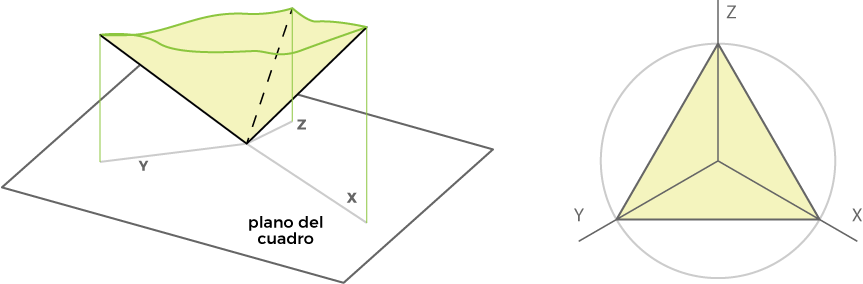
Una de las características fundamentales de todos los sistemas de representación es la reversibilidad del proceso. Arco Díaz (s/f) la define como una condición fundamental, ya que, a partir de un objeto bidimensional el sistema nos permitirá obtener la posición del espacio de cada uno de los elementos que constituyen el objeto, o bien, a partir de un objeto tridimensional, los diferentes sistemas permitirán una representación bidimensional del objeto.
Recapitulando la clasificación antes mencionada, el sistema axonométrico se conforma de los siguientes subsistemas mayormente utilizados:

Proyección paralela perpendicular – Ortogonal
- Subsistema Isométrico
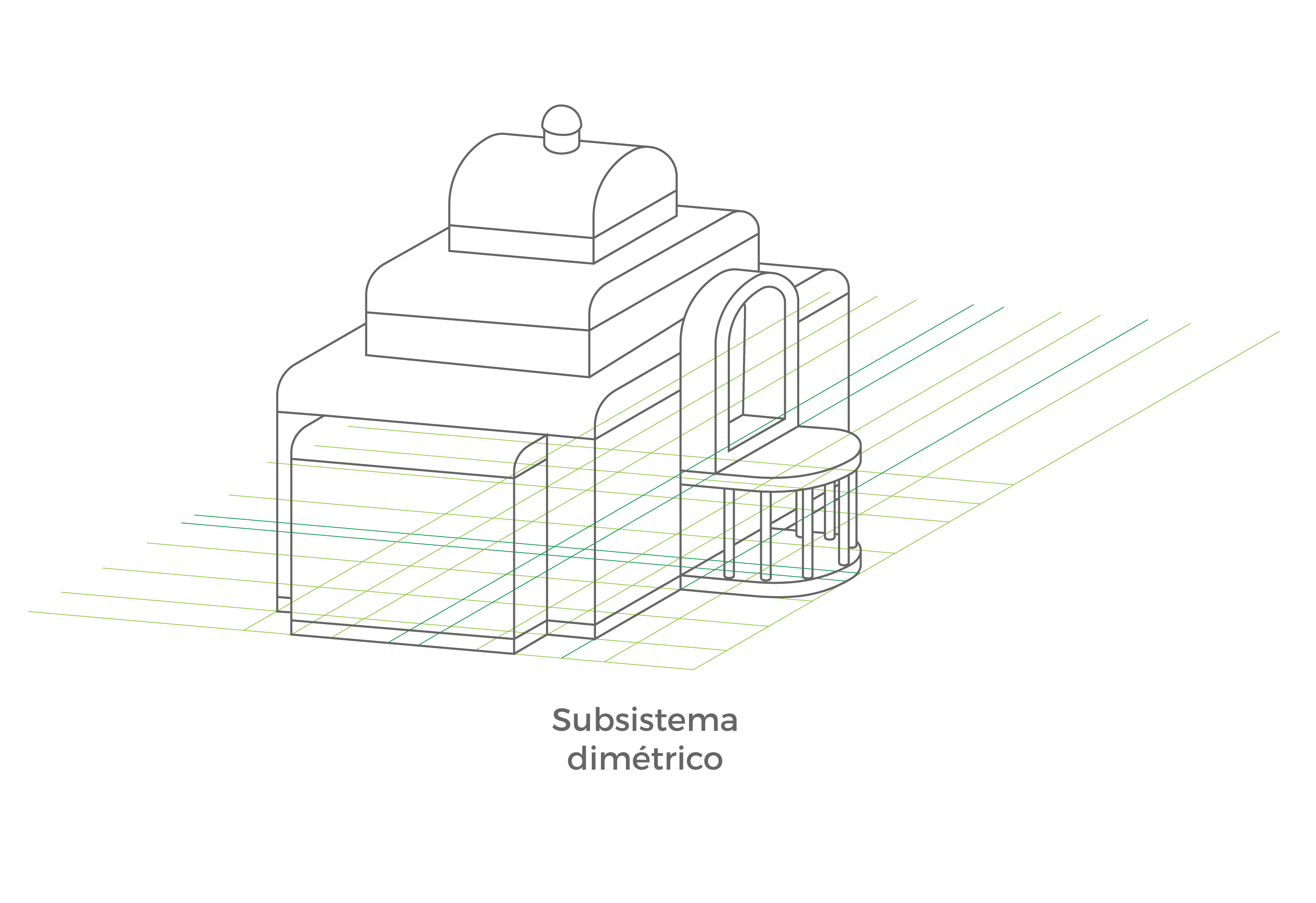
- Subsistema Dimétrico
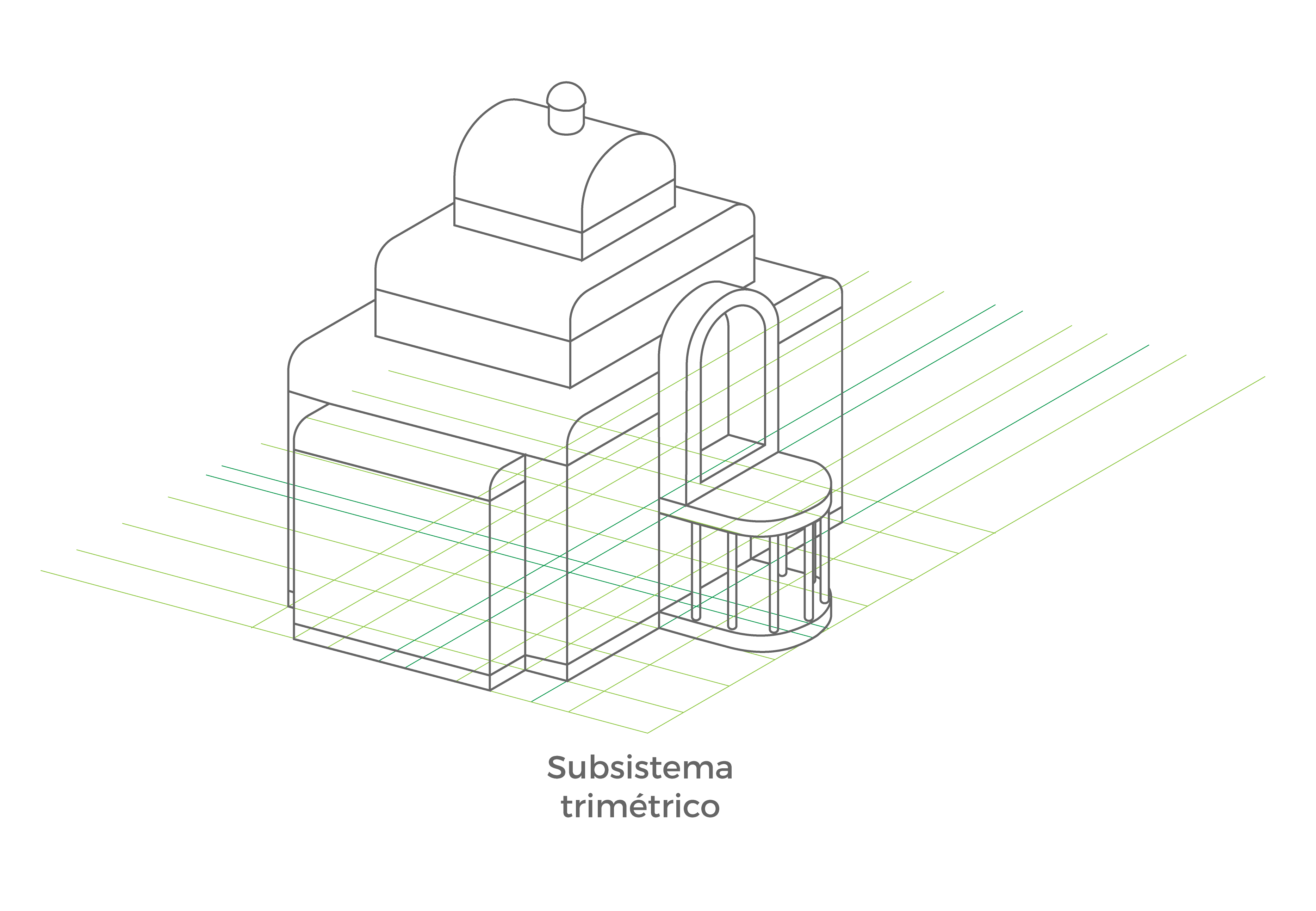
- Subsistema Trimétrico
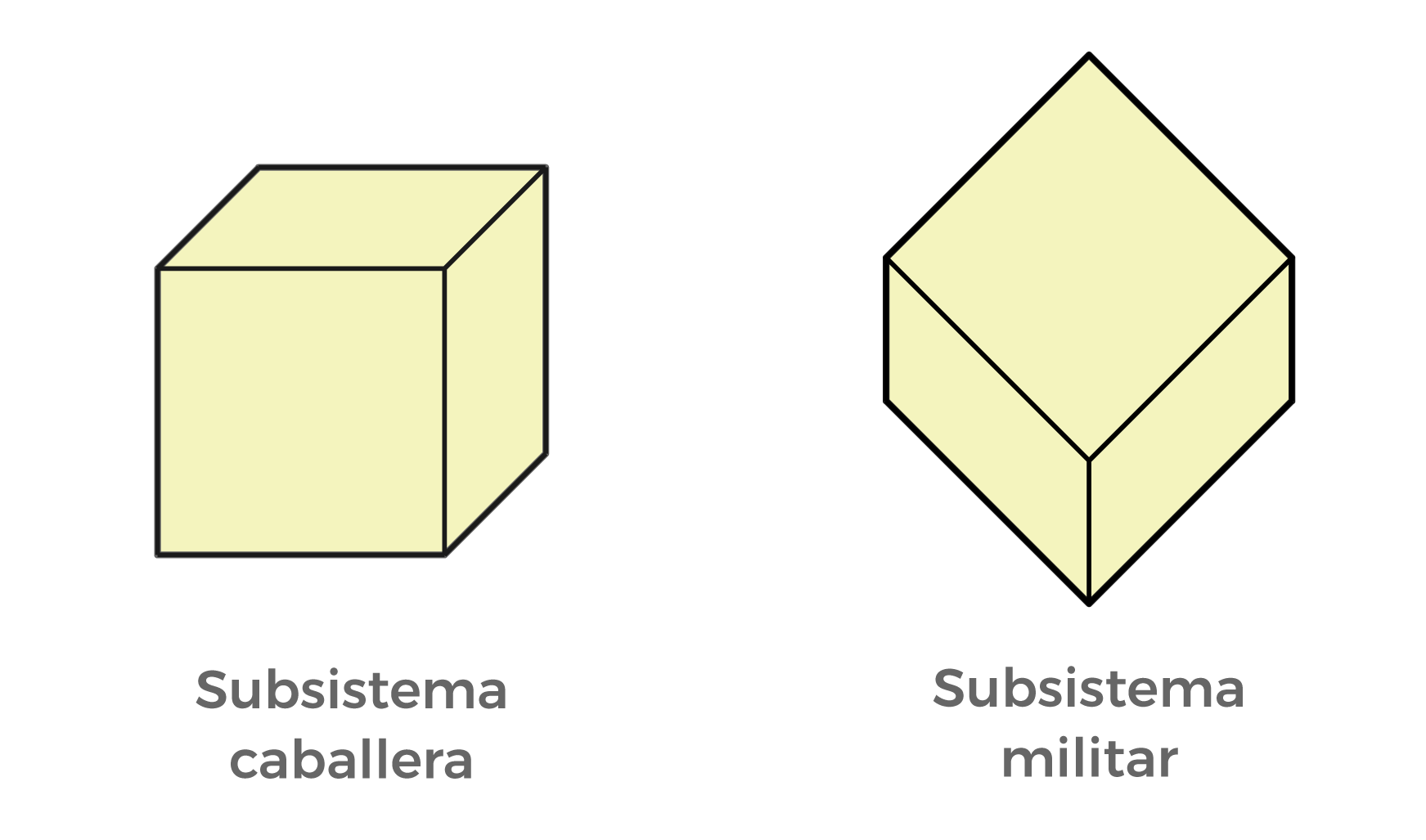
Proyección paralela oblicua
Tiene muchas variantes, algunas de las más conocidas son:
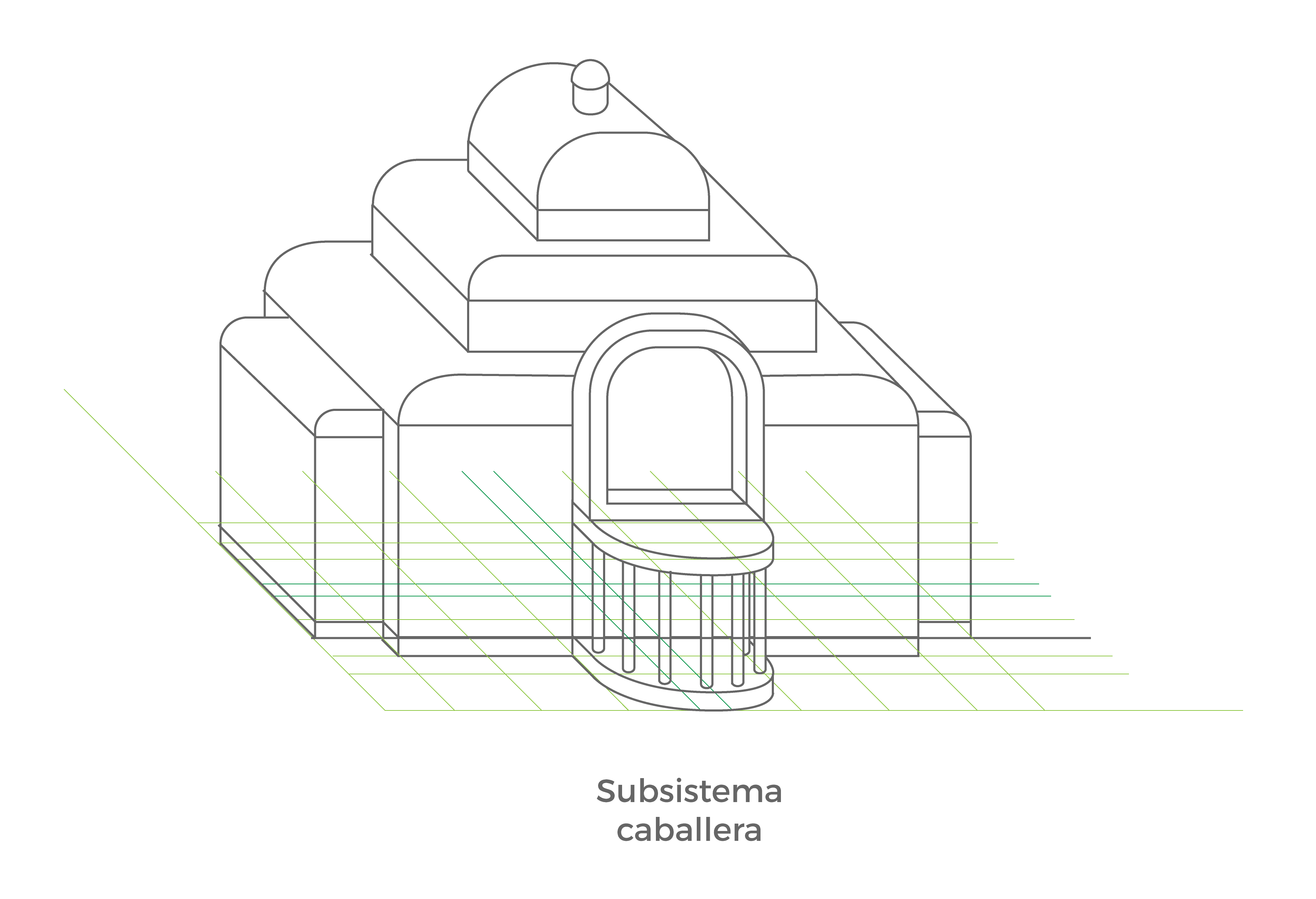
- Subsistema caballera
- Subsistema militar
Subsistemas axonométricos
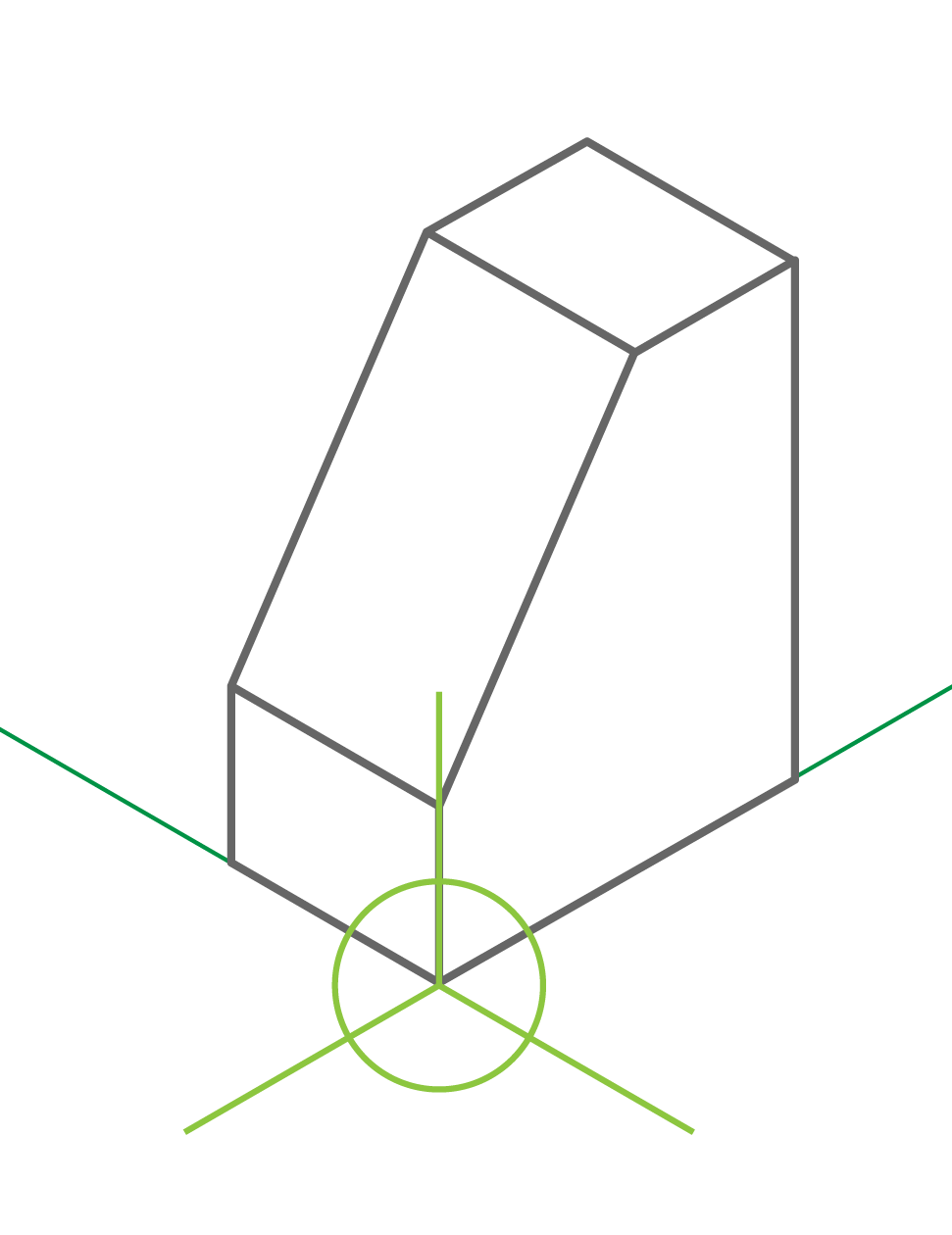
Los tres ejes que constituyen el plano de proyección forman tres ángulos iguales de 120º.
Compensación en las magnitudes:
No tiene variantes. 1:1:1
Vista cenital acentuada.
Forma más frecuente en dibujo técnico.
Poco efecto tridimensional.
Medidas comprensibles.
No adecuado para plantas con simetrías (por ejemplo cubos).
Ángulos
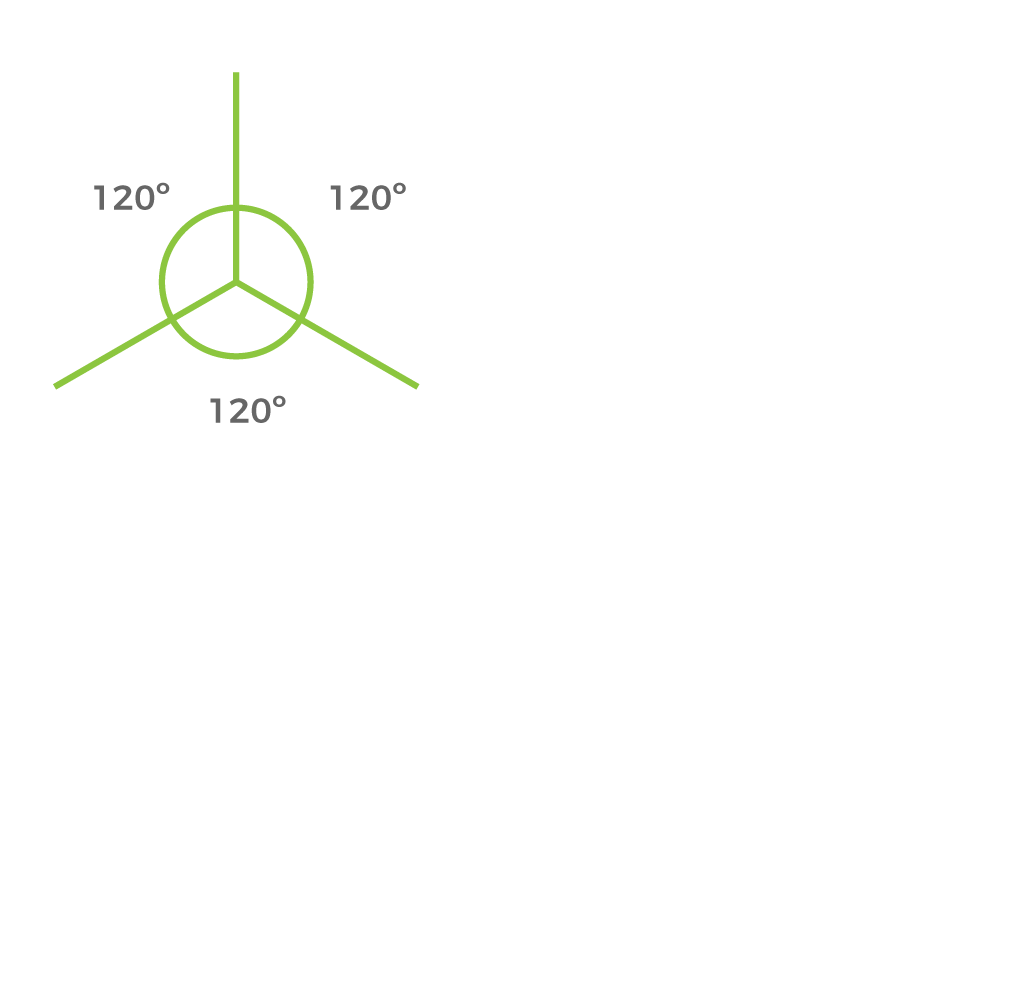
Ejes del dibujo para el volumen ejemplificado
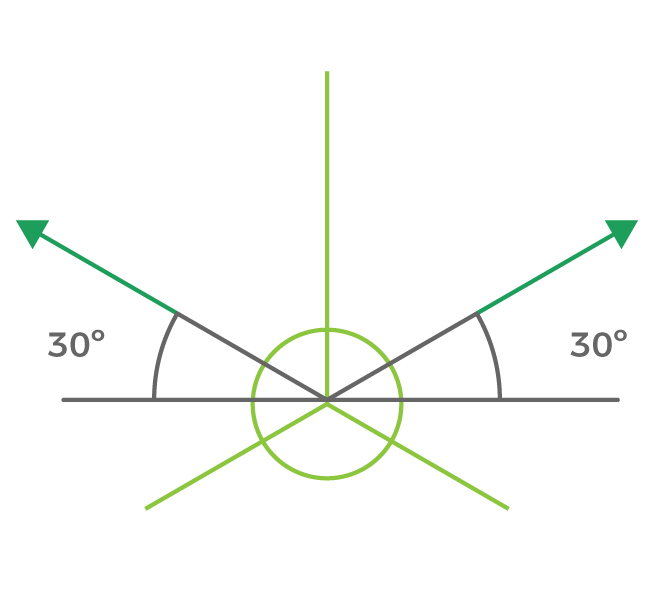
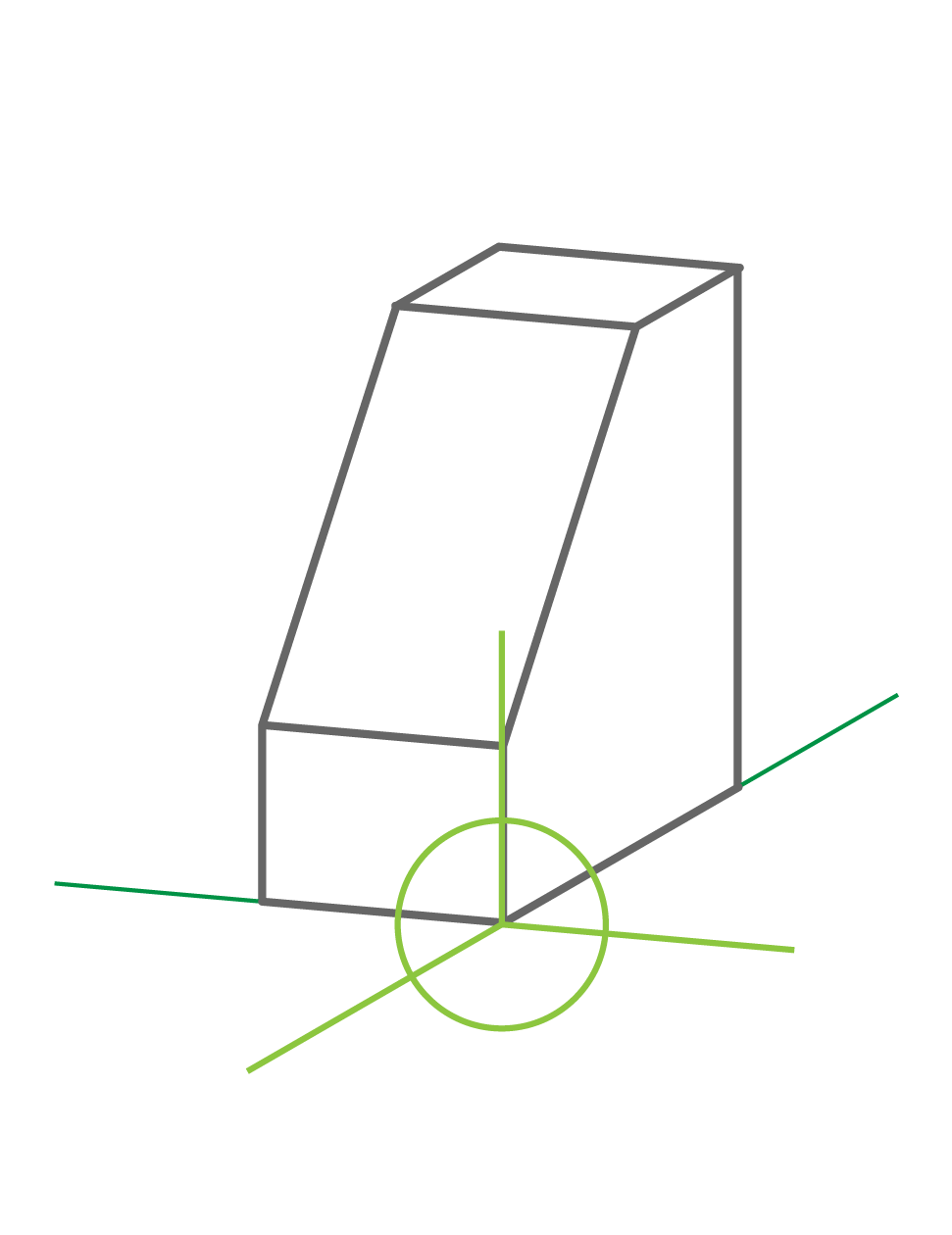
Los tres ejes que constituyen el plano de proyección forman dos ángulos de igual amplitud y un ángulo de amplitud diferente.
Compensación en las magnitudes:
Existen diversas compensaciones dependiendo de los ángulos. Para el caso ejemplificado,
las profundidades se redujeron a 2/3 partes. 1:1:2/3
No se puede hacer la construcción con los ángulos usualmente utilizados en dibujo
lineal.
Apta para representar objetos con una anchura predominante.
Ángulos
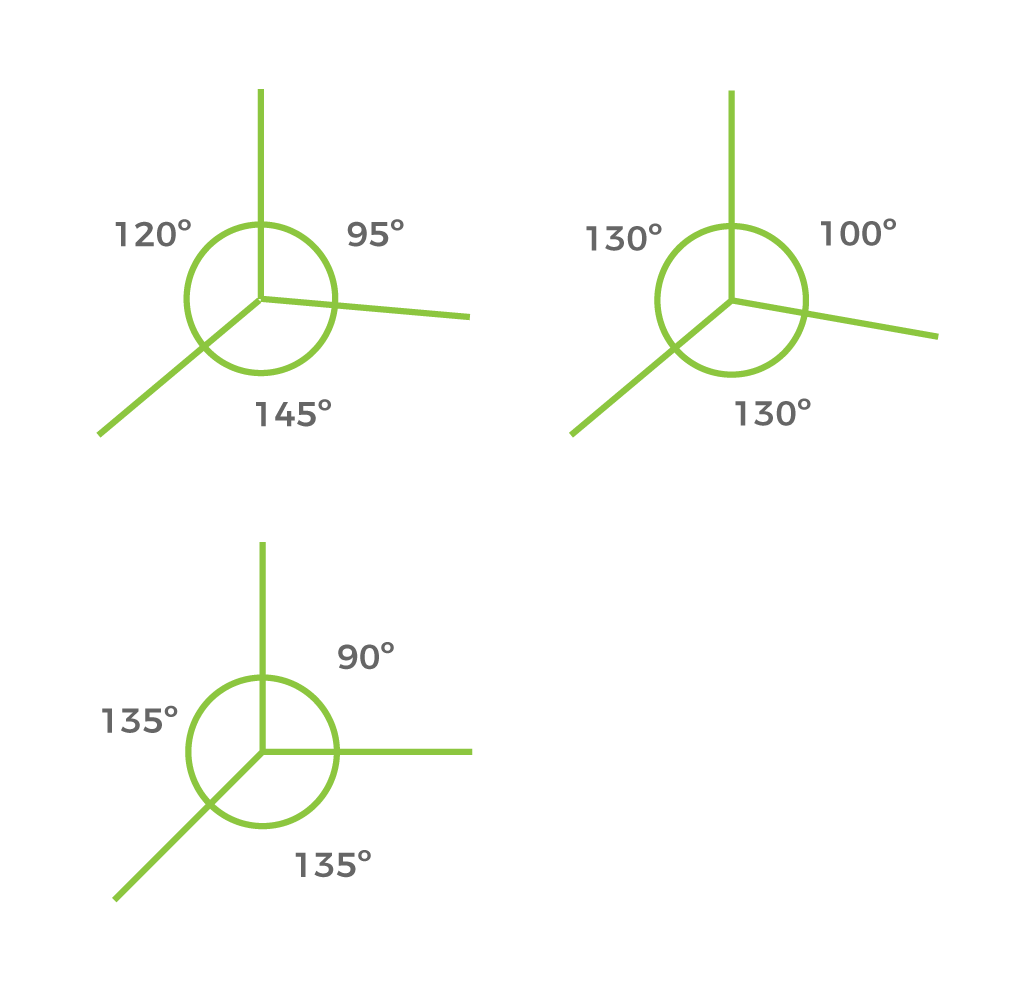
Ejes del dibujo para el volumen ejemplificado
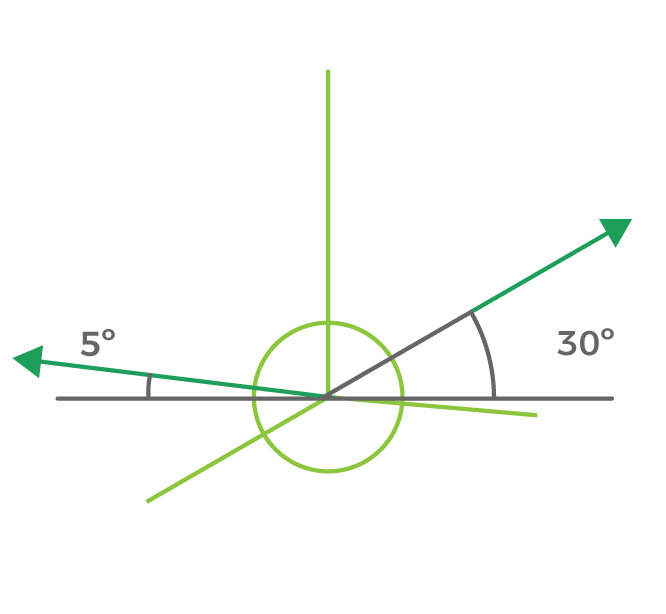
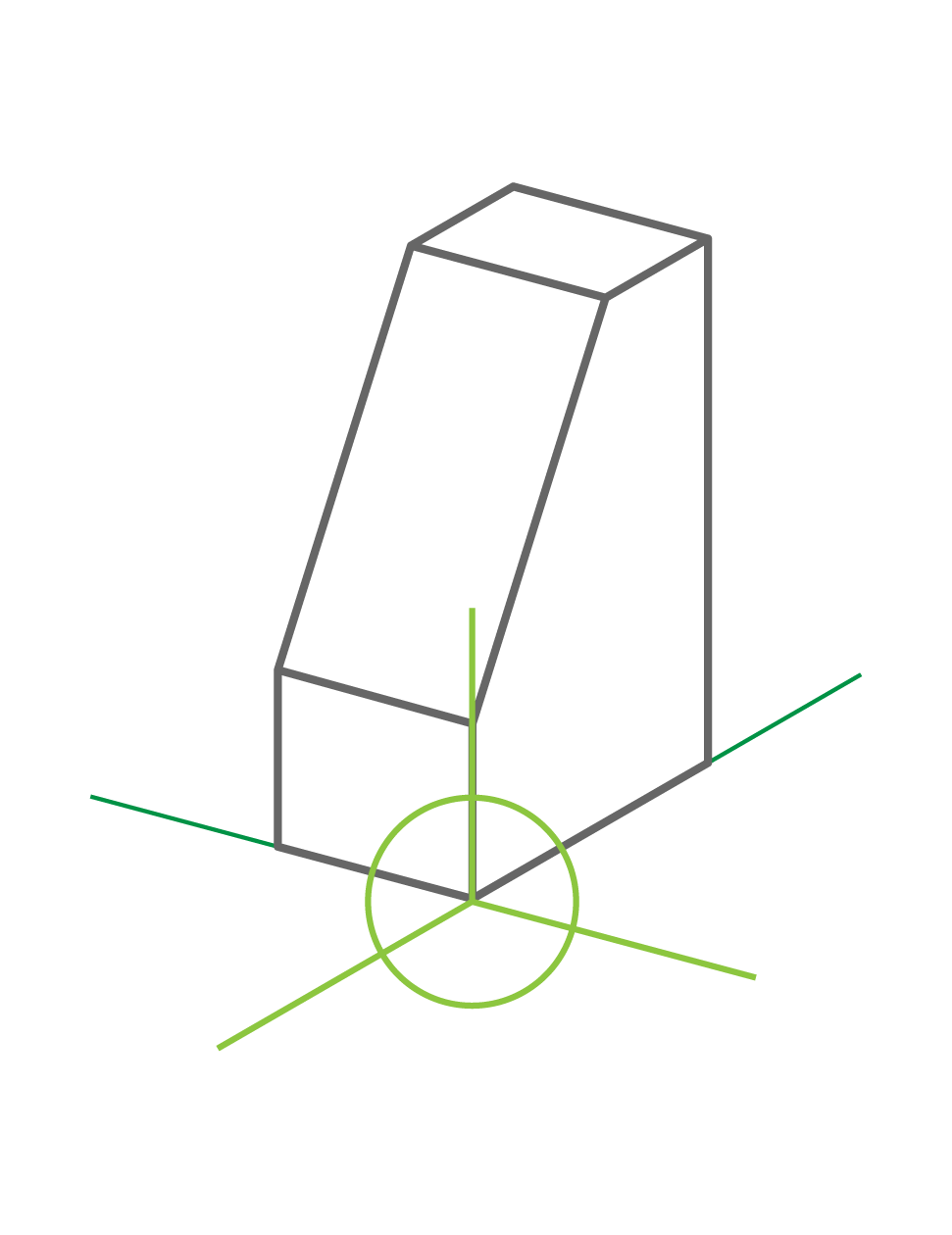
Los tres ejes que constituyen el plano de proyección, forman tres ángulos de amplitud diferente.
Compensación en las magnitudes:
Igual que en el dimétrico existen diversas compensaciones dependiendo de los ángulos, para
este caso, las anchuras se redujeron a 5/6 partes y las profundidades a 2/3 partes.
5/6:1:2/3
Apta para objetos con poca profundidad.
Claridad visual.
Ángulos
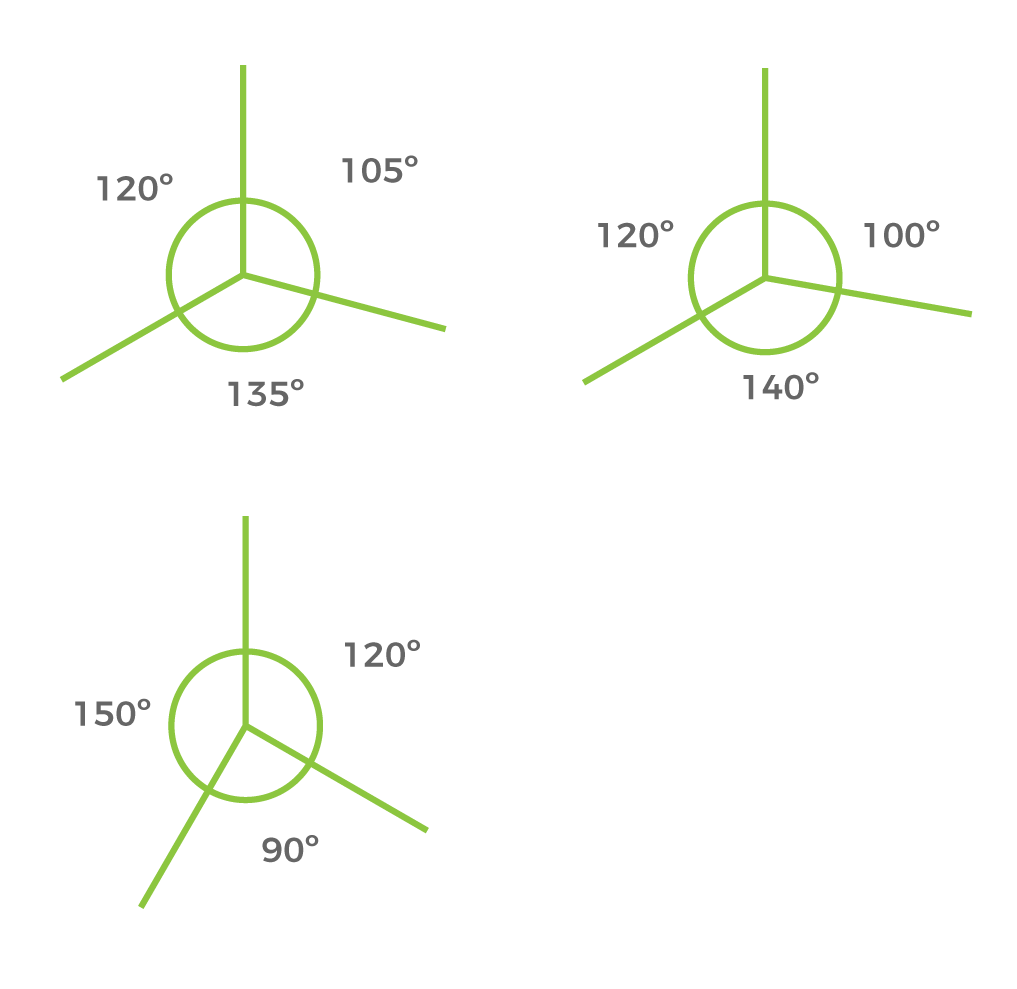
Ejes del dibujo para el volumen ejemplificado
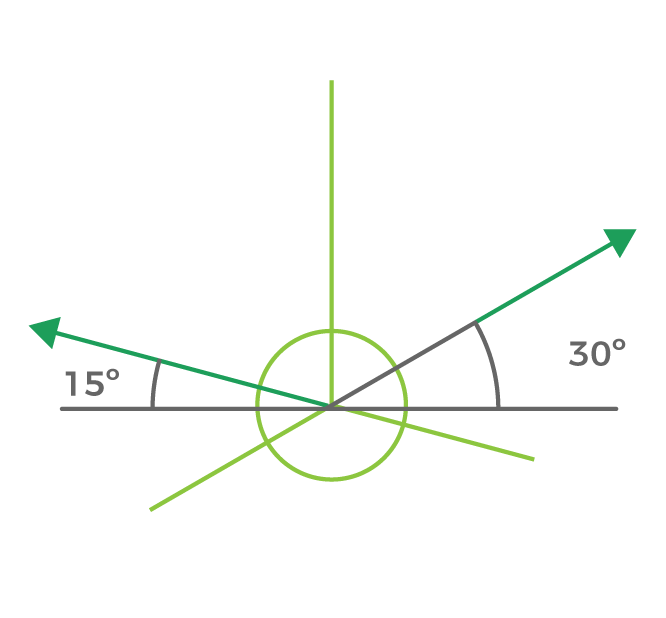
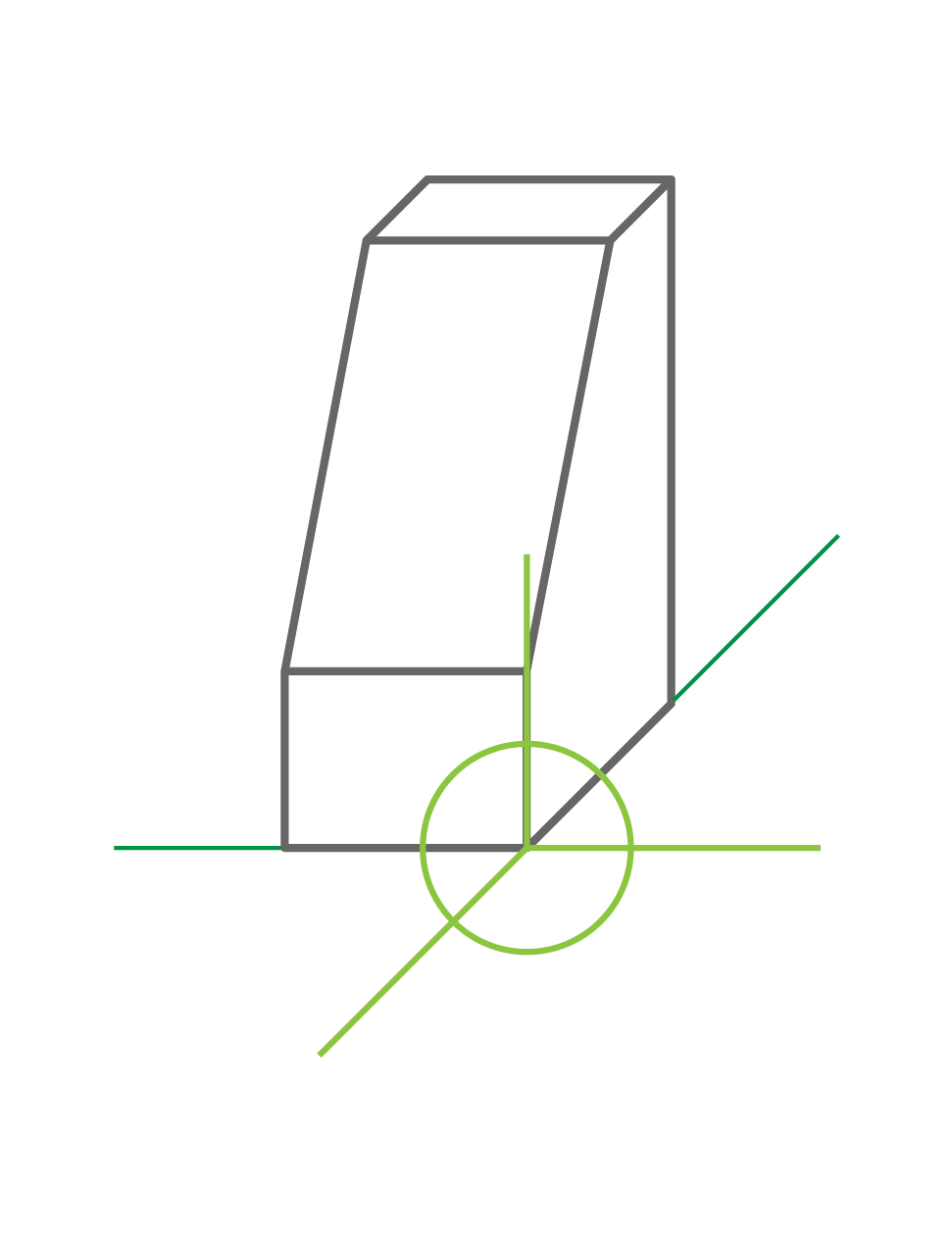
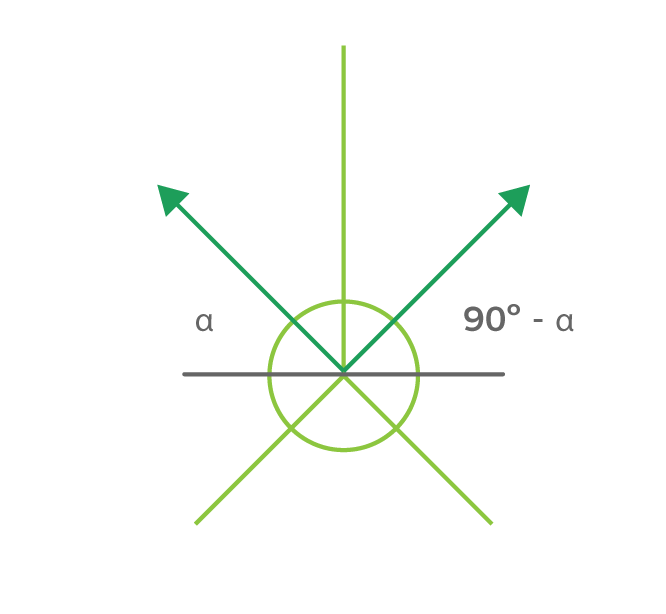
Uno de los ejes que forma el plano se ubica en paralelo al observador, es decir, es completamente frontal. El otro de los ejes tiene una inclinación de 45º.
Compensación en las magnitudes:
Al tener variantes en diversos ángulos, existen diversas escalas.
Generalmente las profundidades se reducen a la mitad. 1:1:1/2
Método de representación sencillo.
Buena claridad visual.
Alzado sin distorsión.
Poco efecto de profundidad.
Ángulos
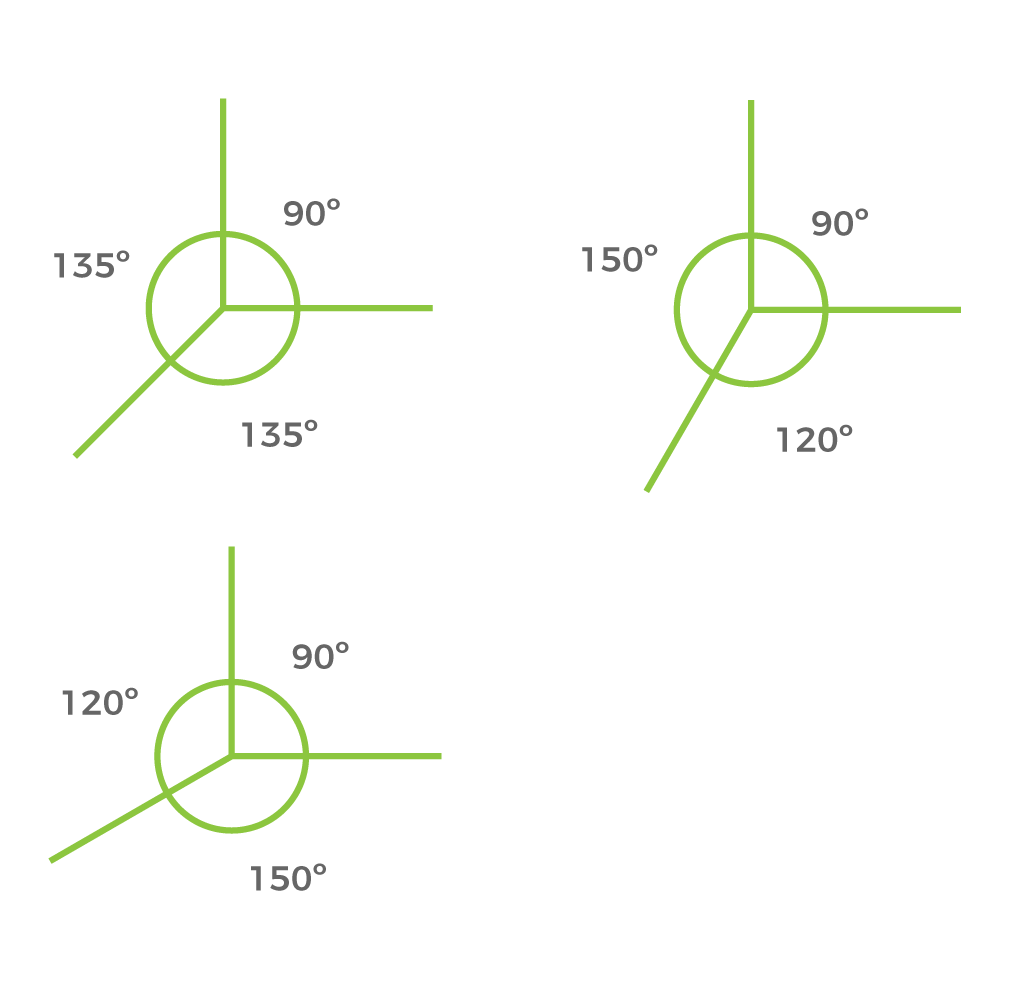
Ejes del dibujo para el volumen ejemplificado
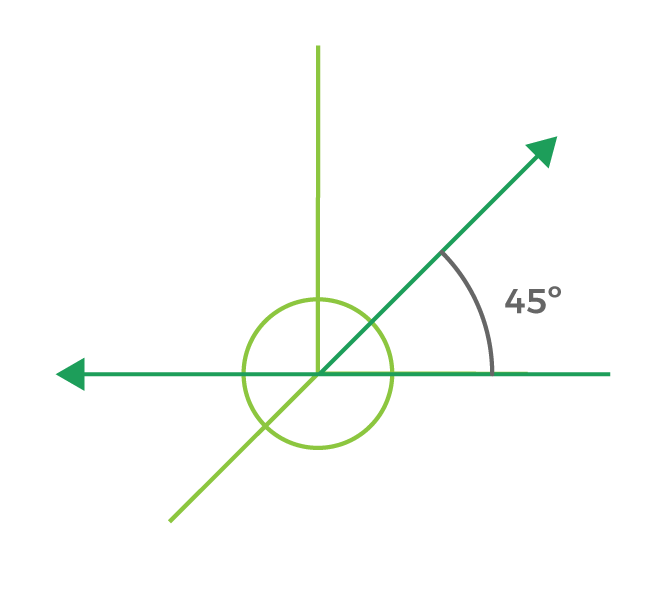
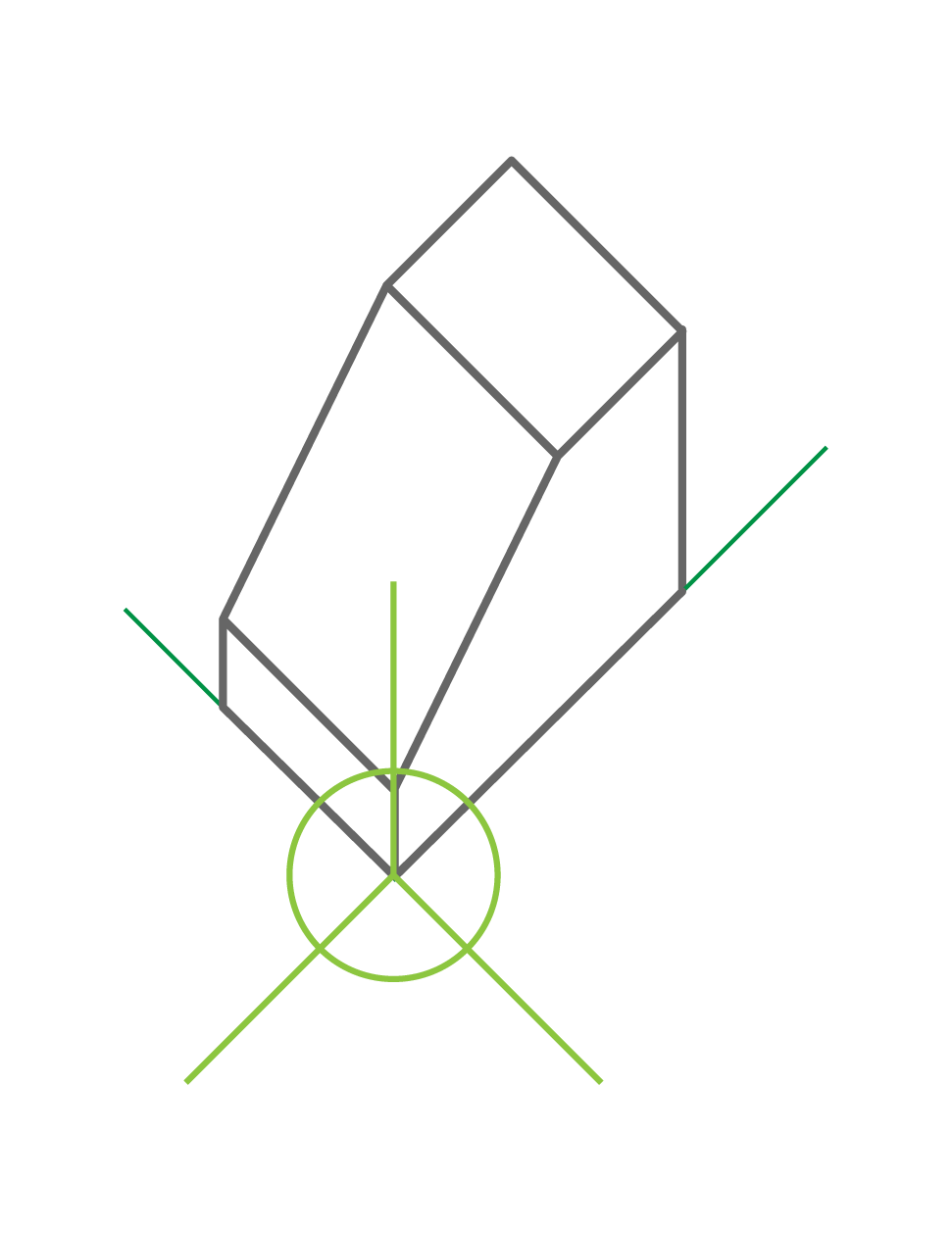
El plano del cuadro conformado por los ejes X y Y forman un ángulo de 90º..
Compensación en las magnitudes:
Al tener variantes en diversos ángulos, existen diversas escalas.
Generalmente las alturas se reducen a la mitad. 1:1/2:1
Planta sin distorsión.
Vista cenital acentuada.
Apta para objetos que no tienen ángulos rectos.
Especialmente adecuada para objetos complejos y edificios.
Es muy usada en las perspectivas de arquitectura e ingeniería civil.
Ángulos
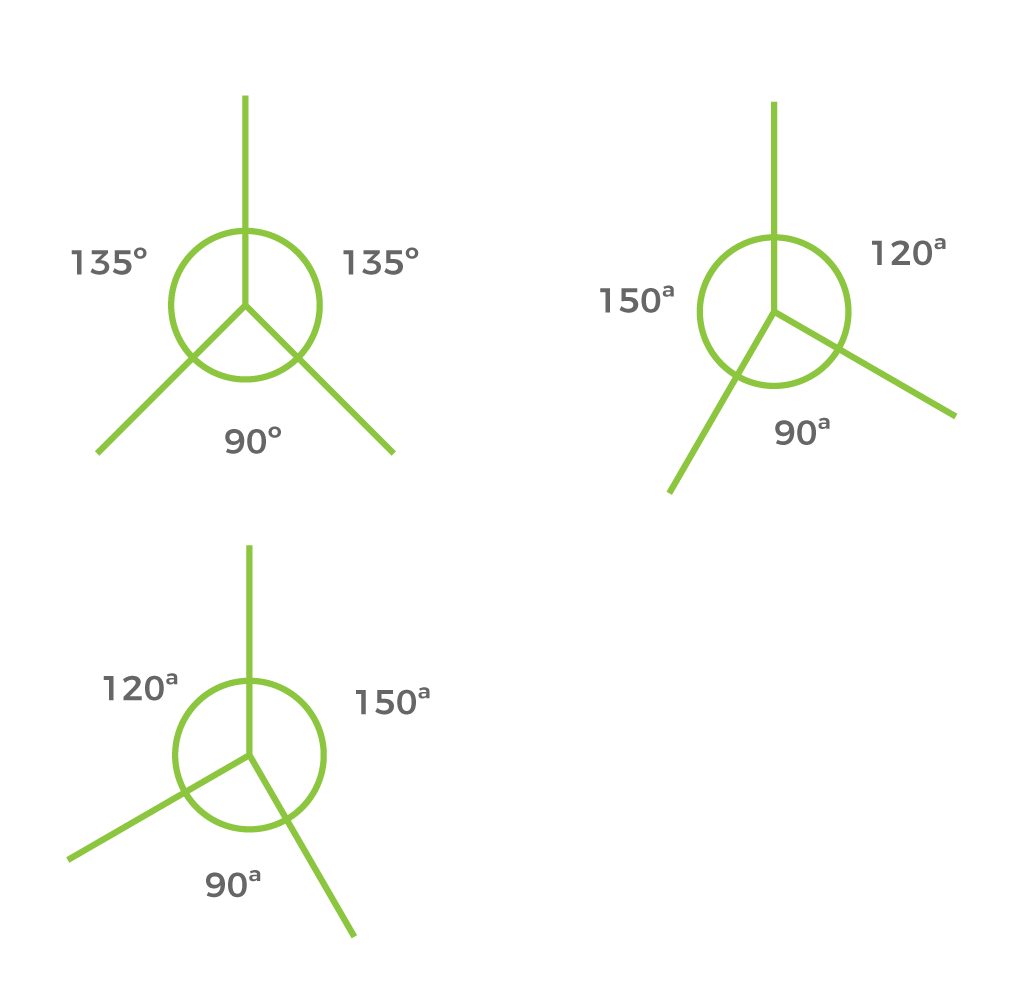
Ejes del dibujo para el volumen ejemplificado
De acuerdo con las características del objeto o volumen a representar o de los detalles que se deseen desatacar será conveniente elegir entre los diversos sistemas de axonométricos, por ejemplo, si es un objeto muy simétrico será conveniente no utilizar el subsistema isométrico, de igual forma si son varios volúmenes u objetos y no se encuentran alineados en ángulos rectos, será conveniente utilizar un subsistema militar. Cada uno de los subsistemas tiene diversos grados de inclinación en sus ejes y, por lo tanto, muestran el mismo objeto, pero de distinta forma.
A continuación, se muestra un objeto de mayor complejidad representado en los diversos sistemas, servirá para que observes las diferencias en la inclinación de los ejes en su construcción y para que puedas observar claramente las diferencias de representación en cada una de ellas.
A manera de resumen:
FUENTES DE INFORMACIÓN
Arco Díaz, J. (s/f). Lección 9. Sistemas de representación. En: Dibujo arquitectónico I. España: Universidad de Granada. Disponible en: https://www.ugr.es/~agomezb/etsie_eg1/etsie_eg1_material_docente/t1_3_siste mas_representacion.pdf
Ramos García, F. (1976). Prácticas de dibujo arquitectónico. Barcelona: Gustavo Gili.
Reiner Thomae. (1978). Perspectiva y axonometría. México: Gustavo Gili.
Schimint, Rudolf. (1980). Geometría Descriptiva de figuras estereotómicas. Barcelona: Riverte.