Subsistema caballera y militar

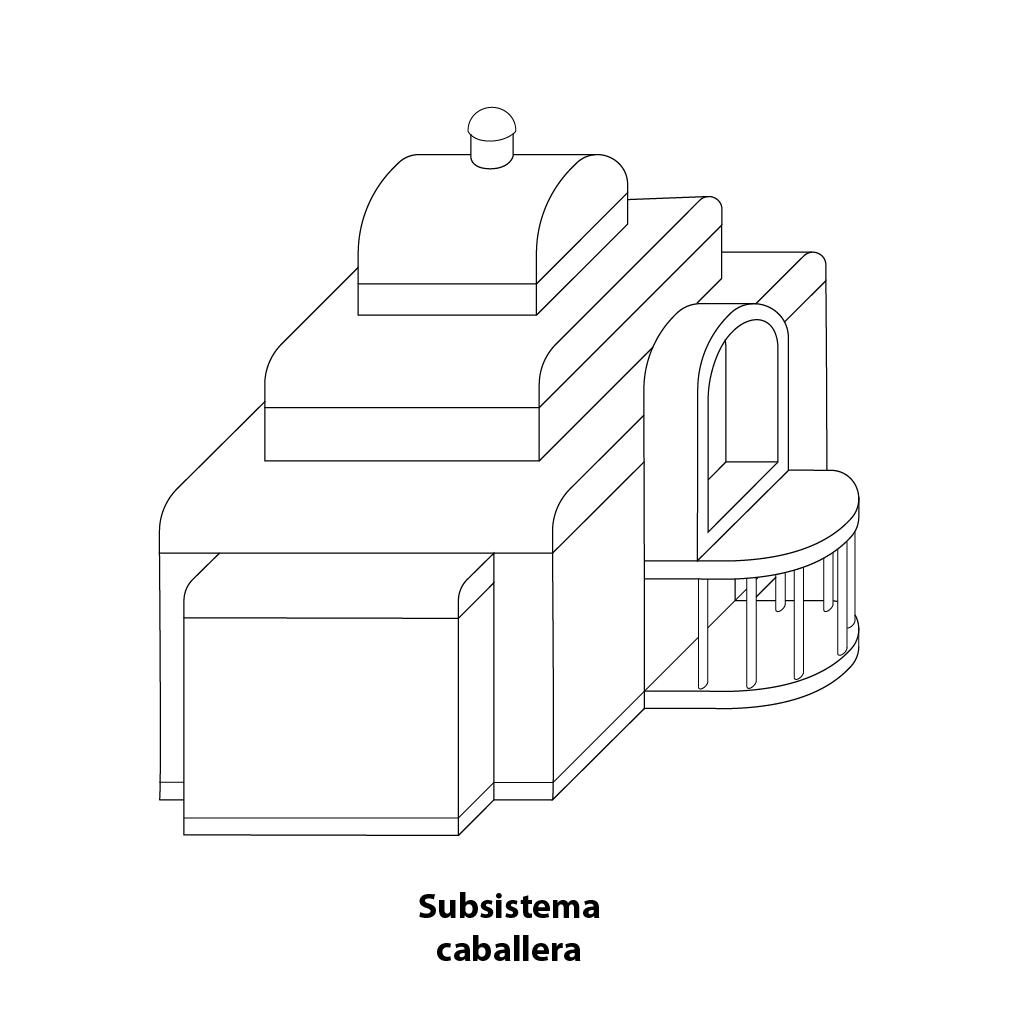
Caballera

Una axonometría caballera consiste en una representación gráfica de un objeto tridimensional de manera bidimensional, la cual tiene como característica la representación de los objetivos desde un punto de vista que asemeja el de un hombre de pie y de frente.

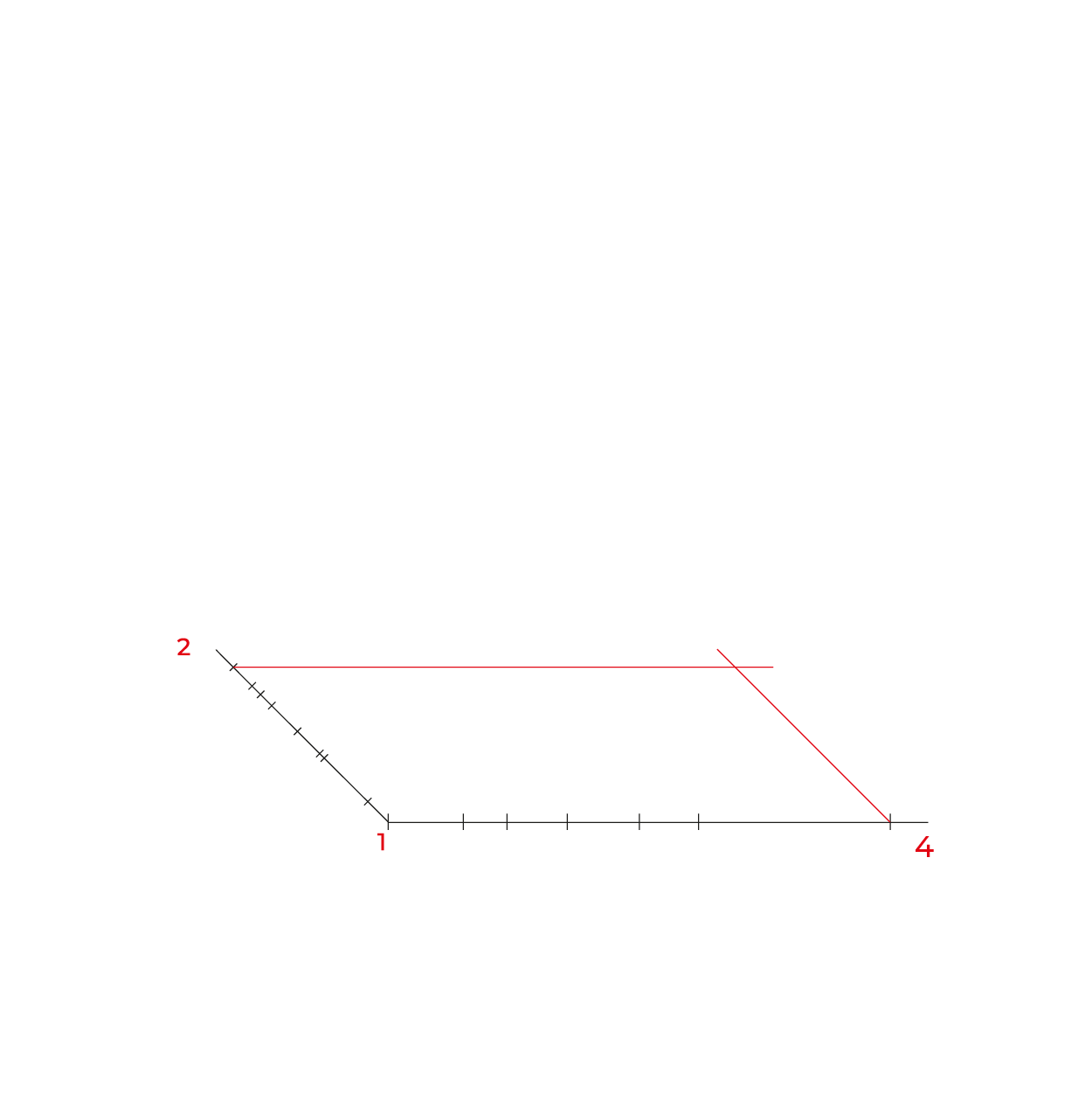
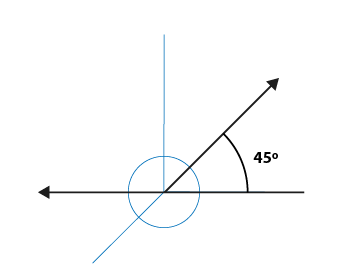
En éste tipo de representación uno de los ejes que forman el plano se ubica paralelo al observador, es decir, es completamente frontal. El otro de los ejes tiene una inclinación de 45º.

Las dimensiones correspondientes a cada uno de los ejes se manejan en dos escalas, es decir, existe una reducción en las profundidades a ½ de la magnitud verdadera, conservando las profundidades en verdadera magnitud.

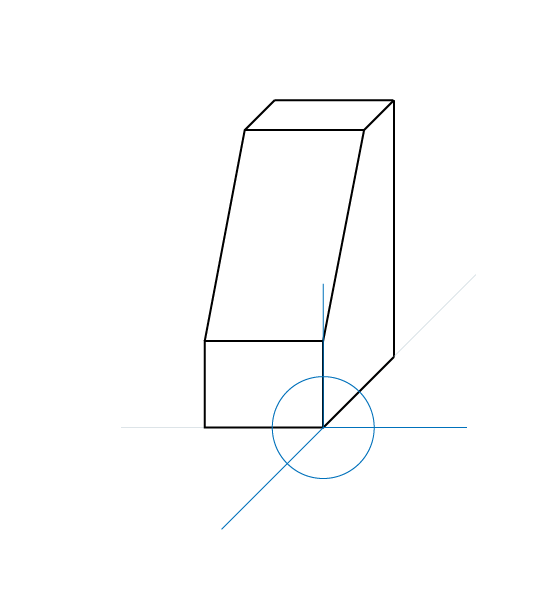
Uno de los ejes que forma el plano se ubica en paralelo al observador, es decir, es completamente frontal. El otro de los ejes tiene una inclinación de 45º.

Compensación en las magnitudes:
Al tener variantes en diversos ángulos, existen diversas escalas.
Generalmente las profundidades se reducen a la mitad. 1:1:1/2

Buena claridad visual.
Alzado sin distorsión.
Poco efecto de profundidad.

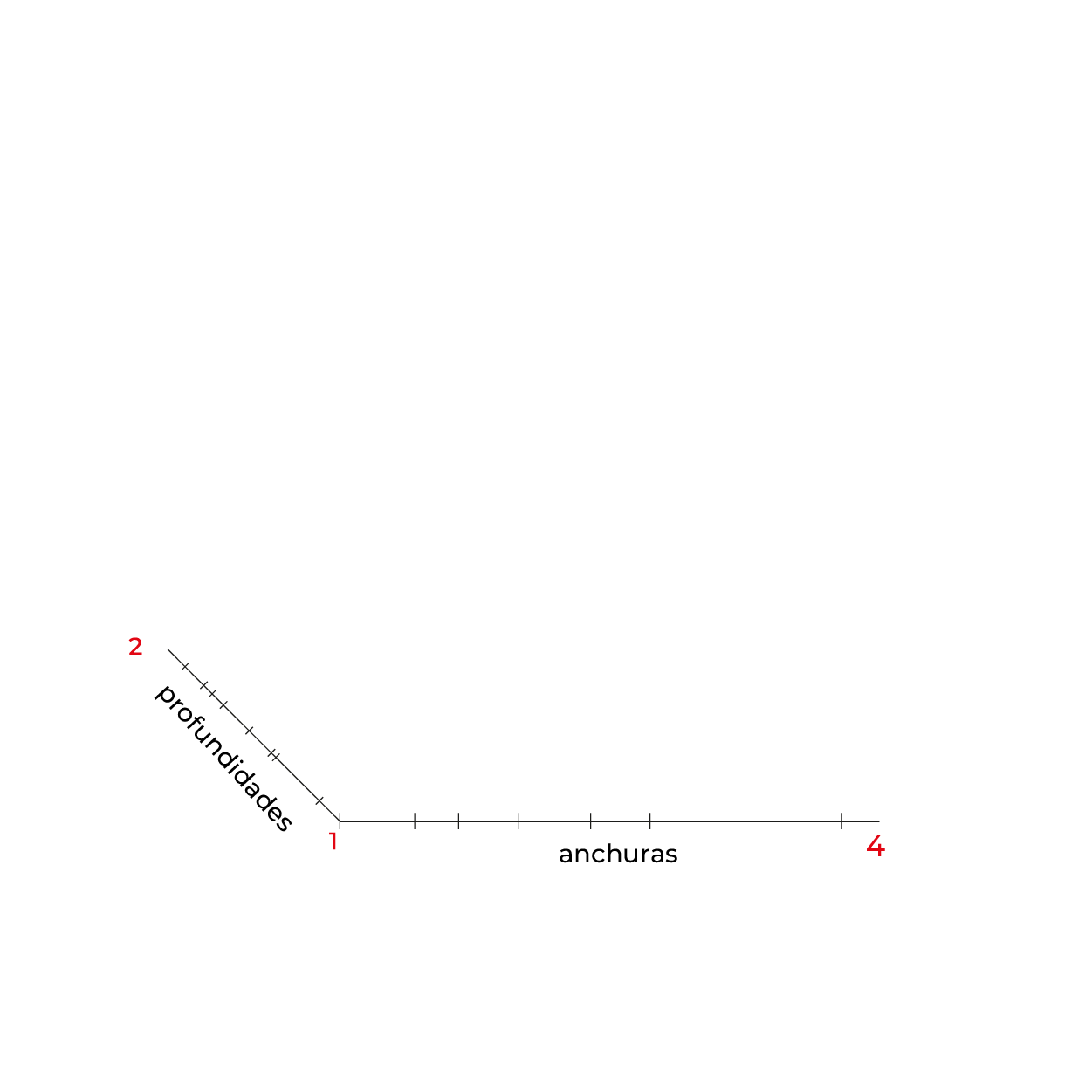
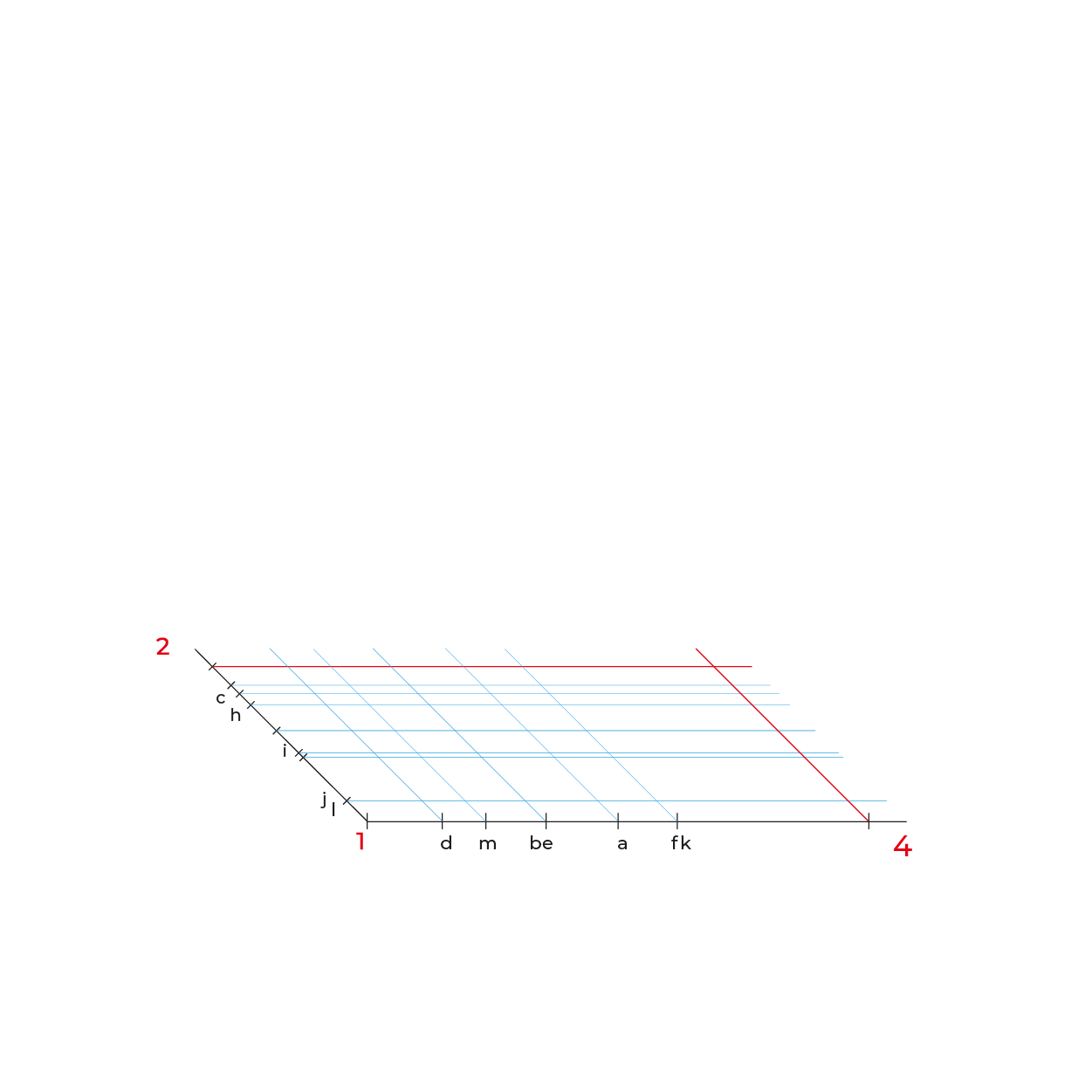
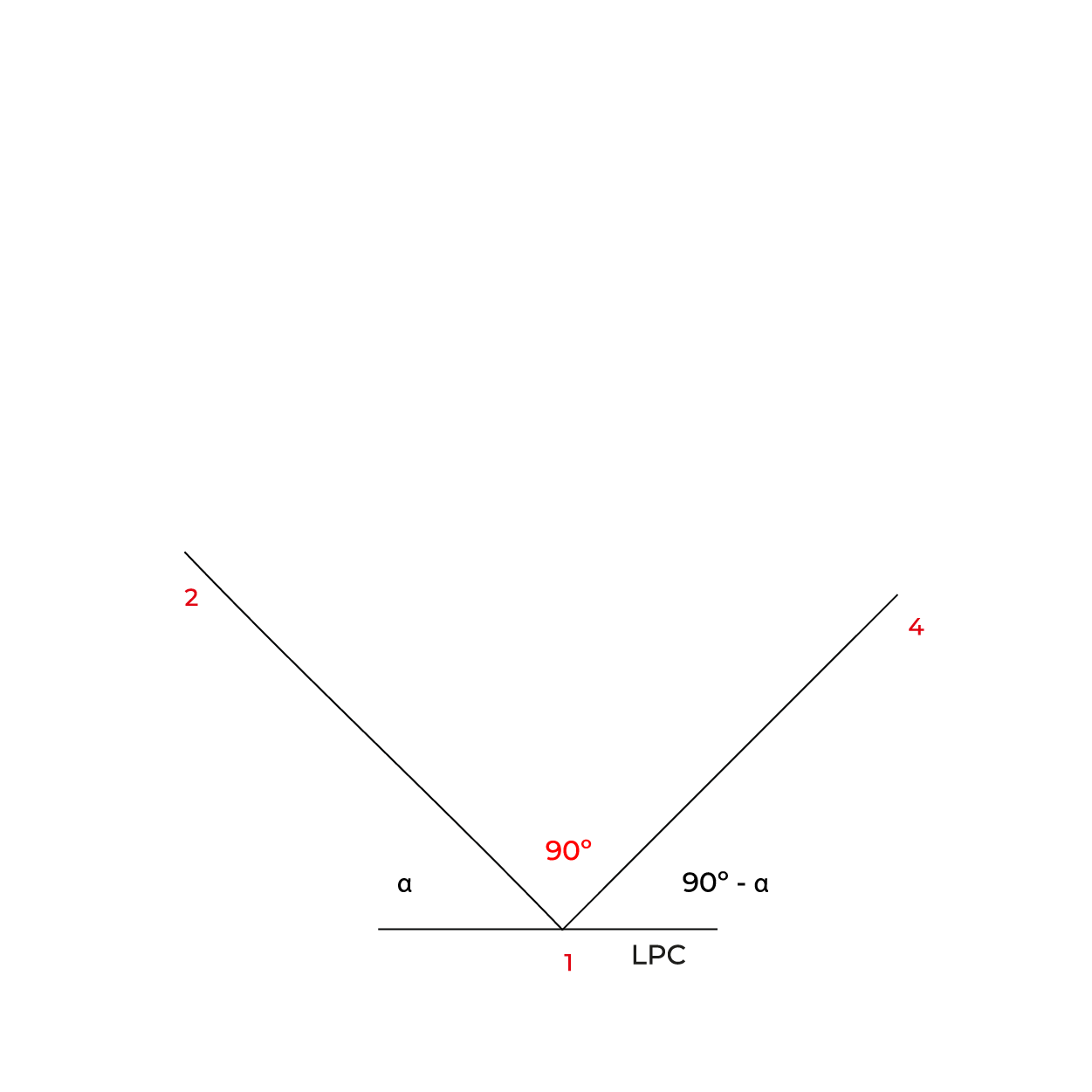
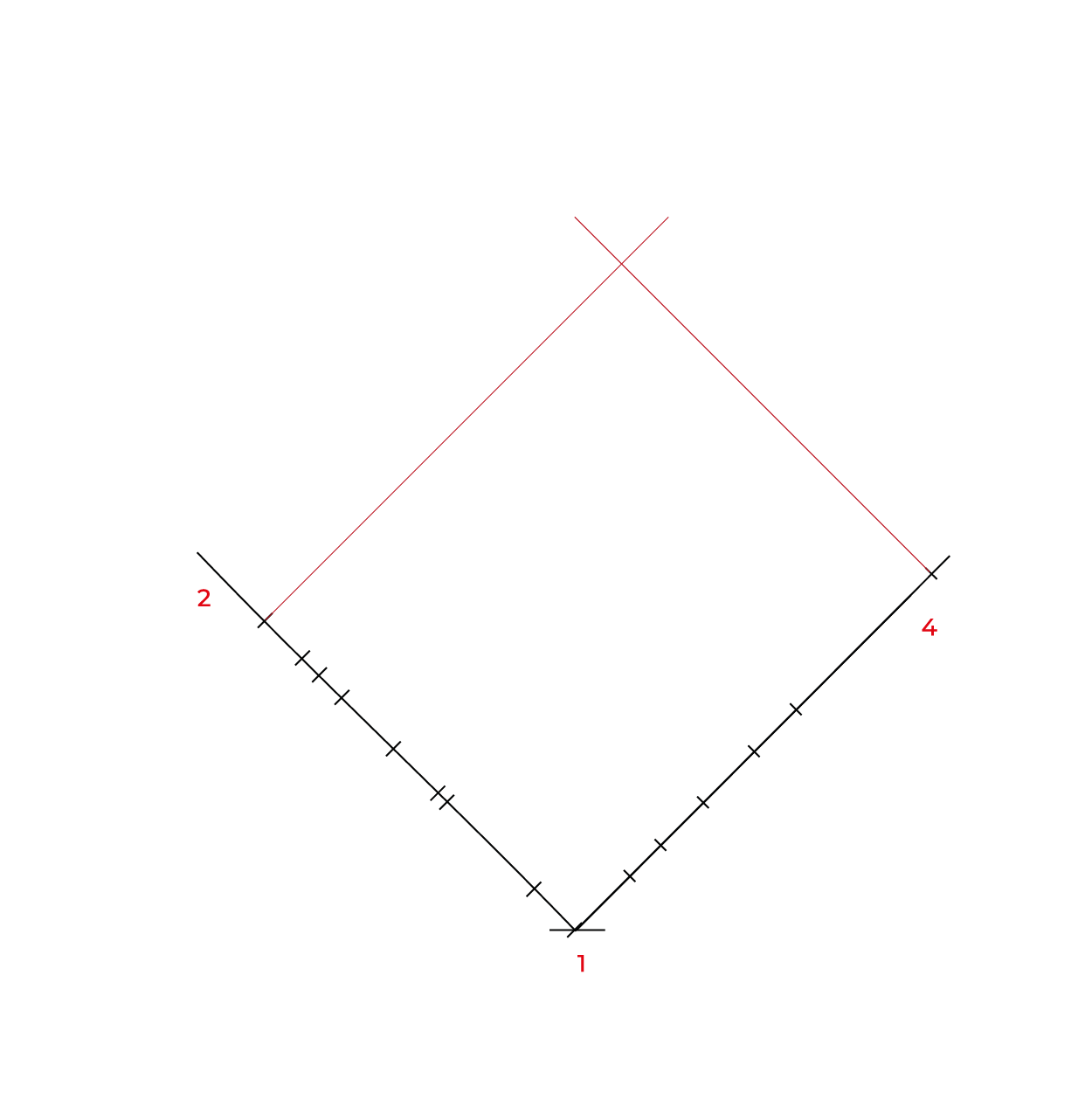
Ángulos que utilizaremos para construcción del plano geometral

Ángulos empleados para la construcción del subsistema caballera

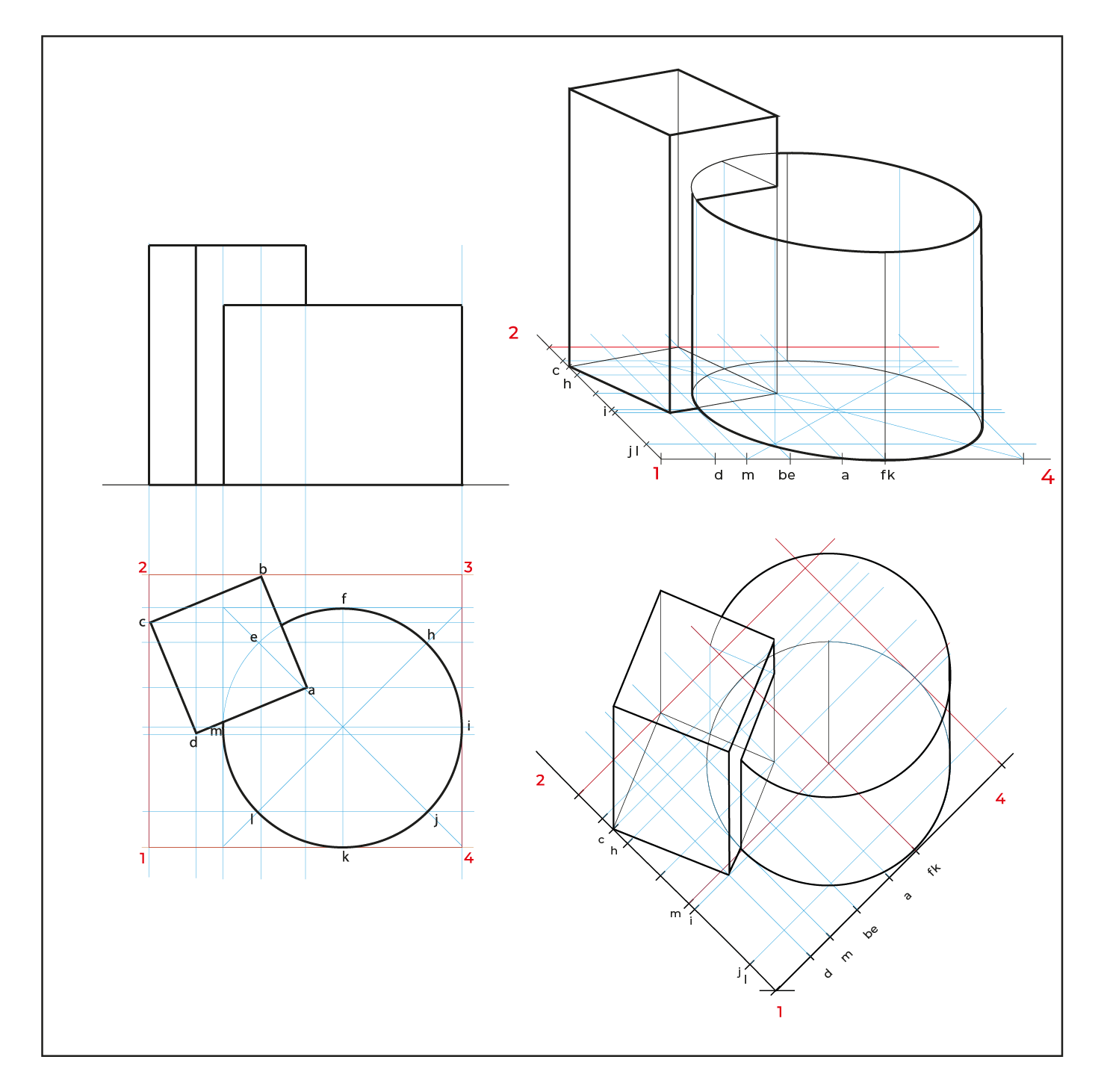
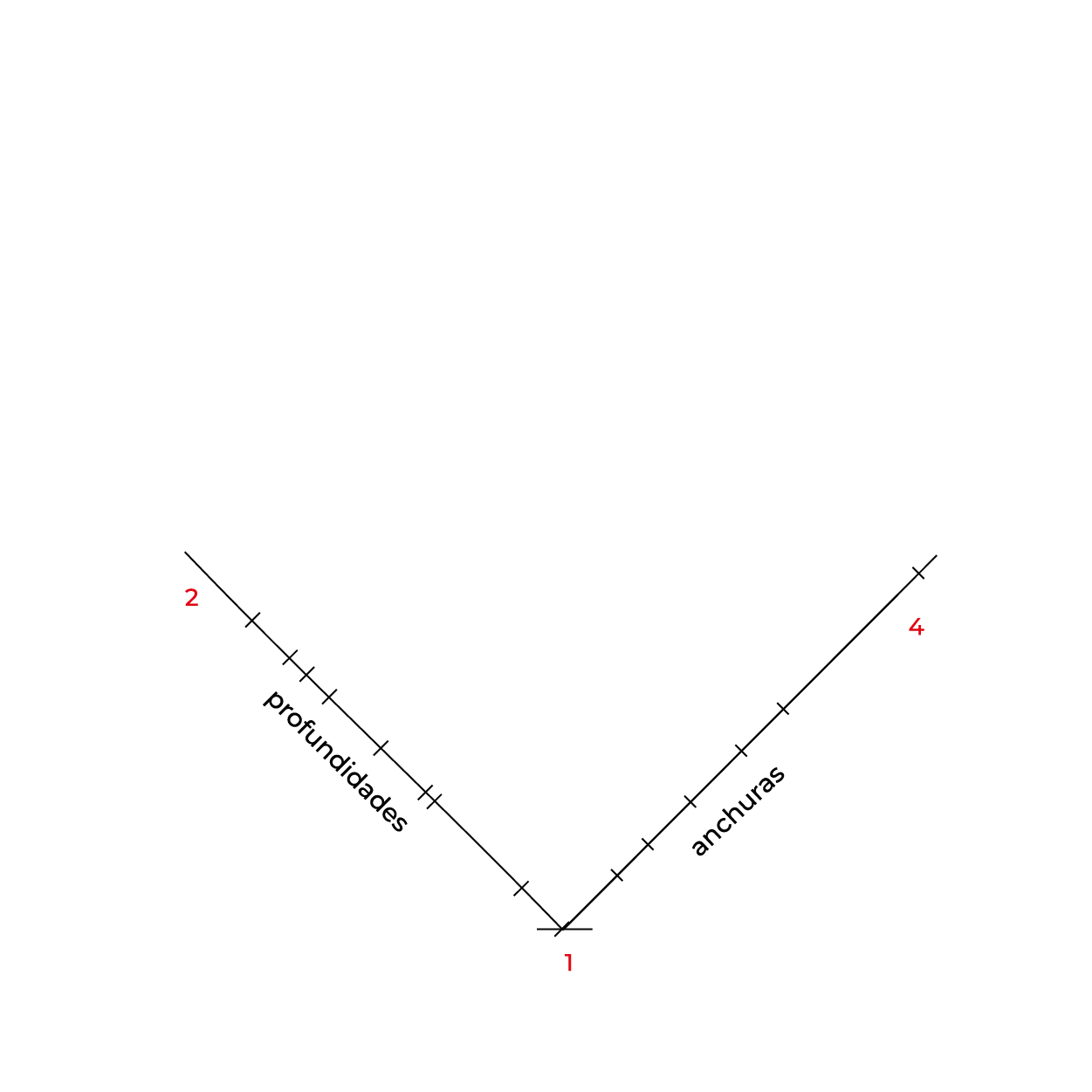
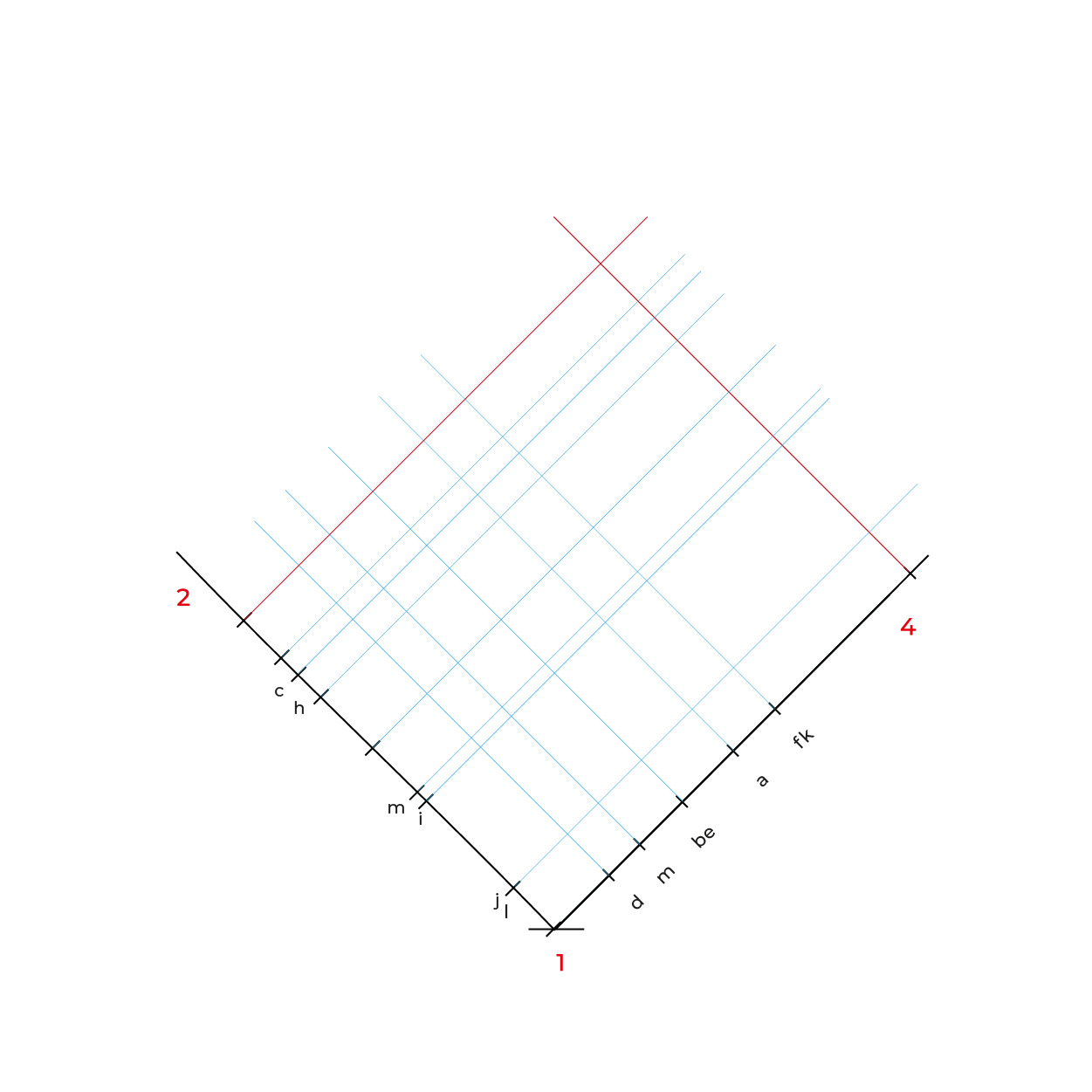
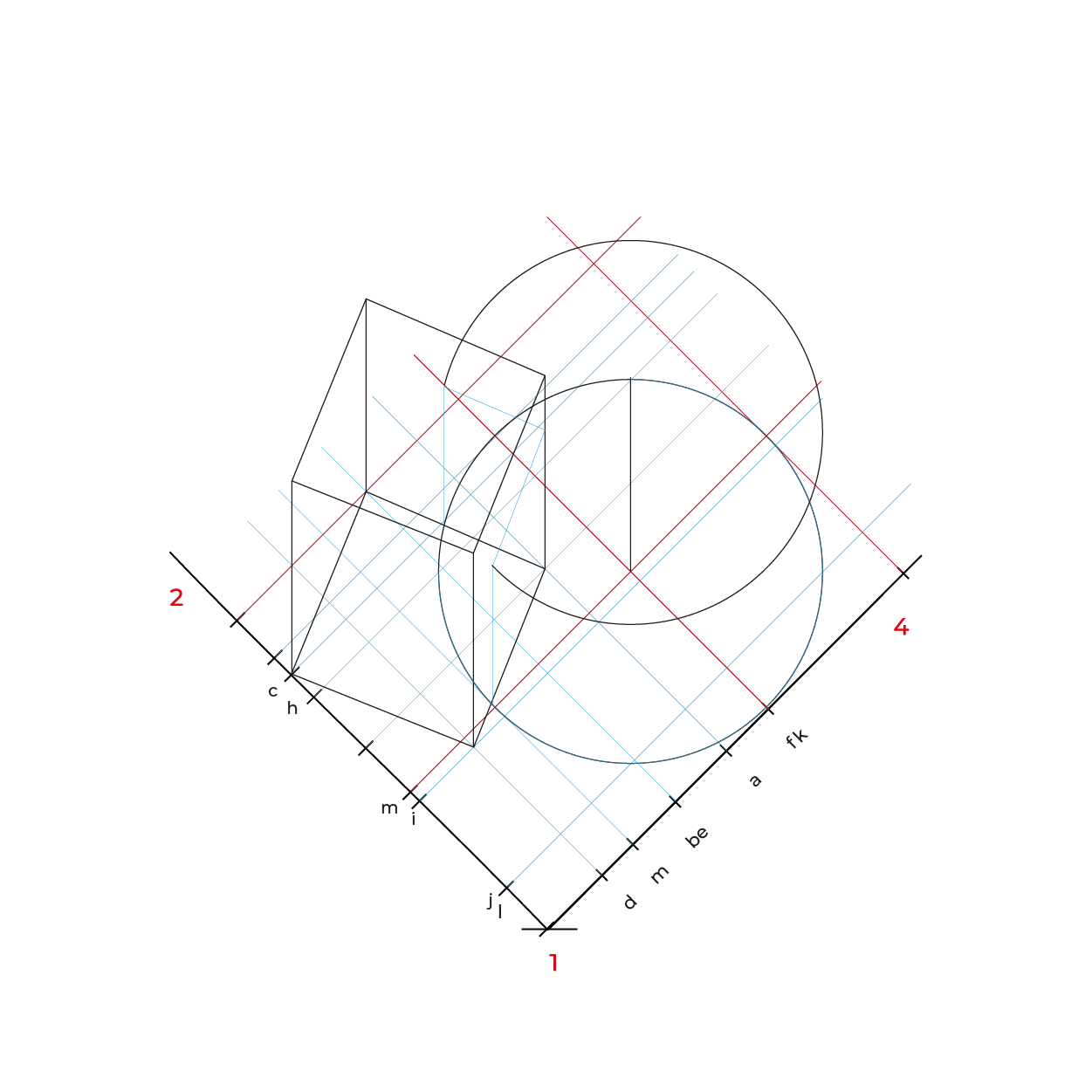
Método por coordenadas

Consideraciones:

Montea biplanar no es necesaria la vista auxiliar.
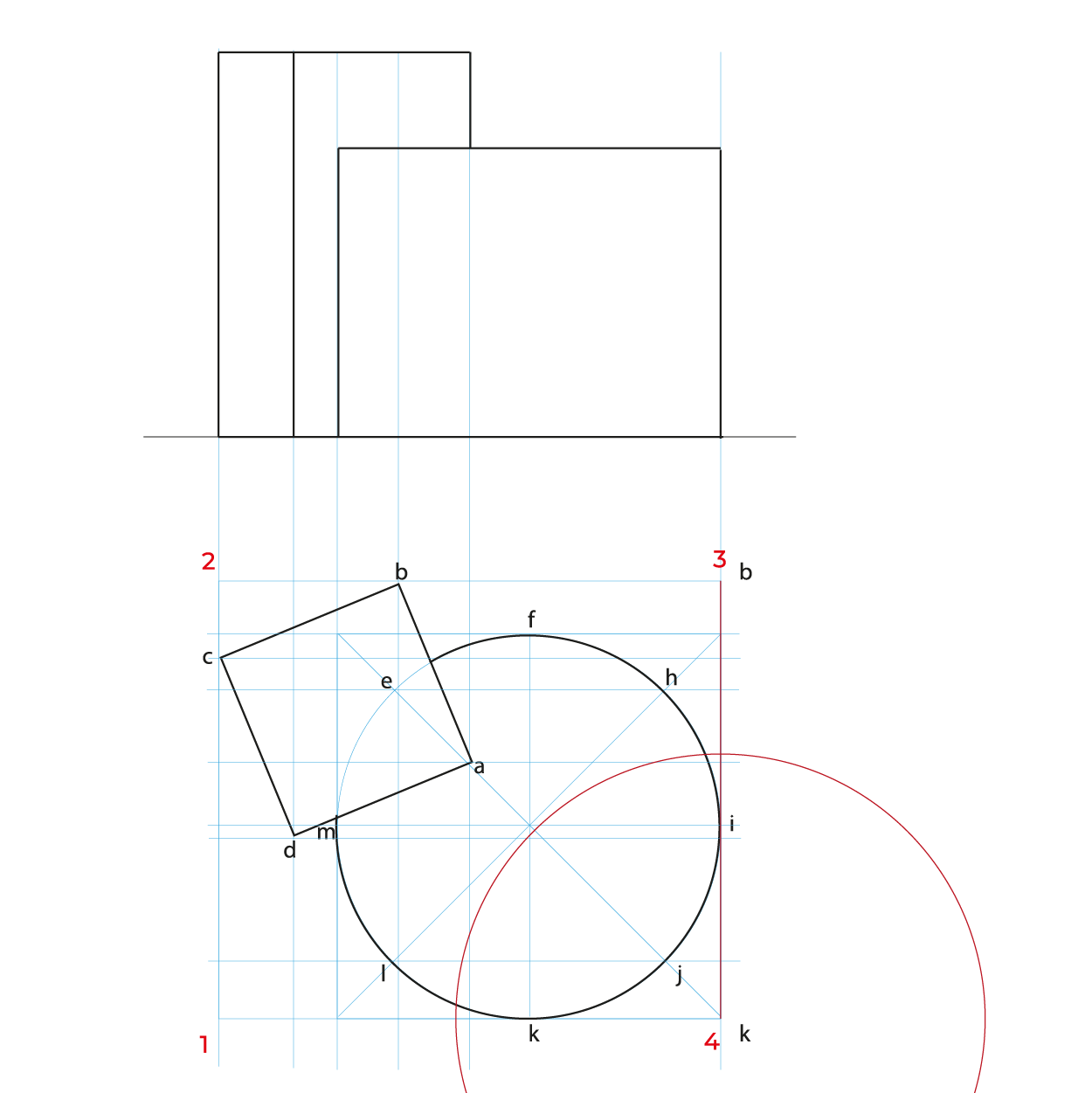
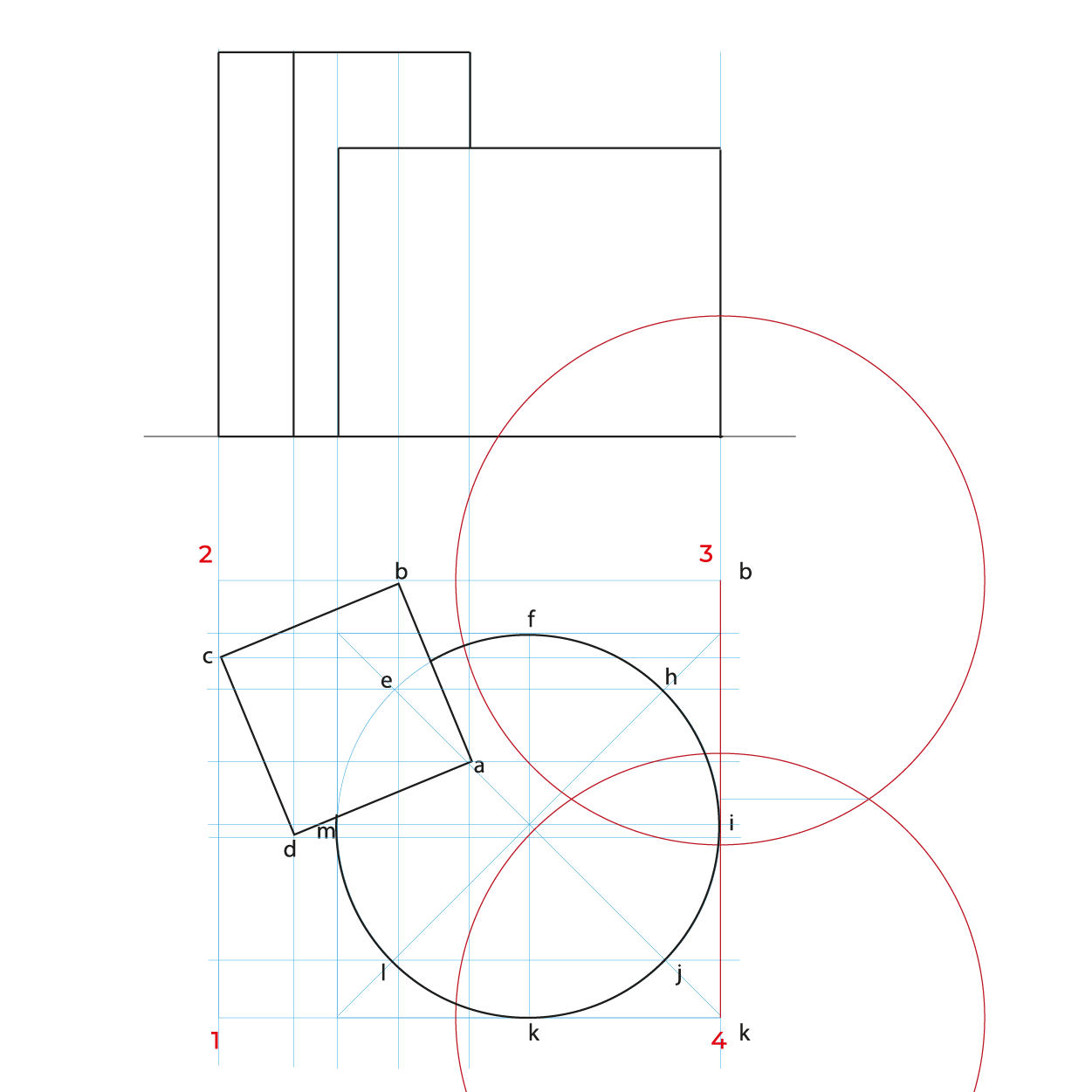
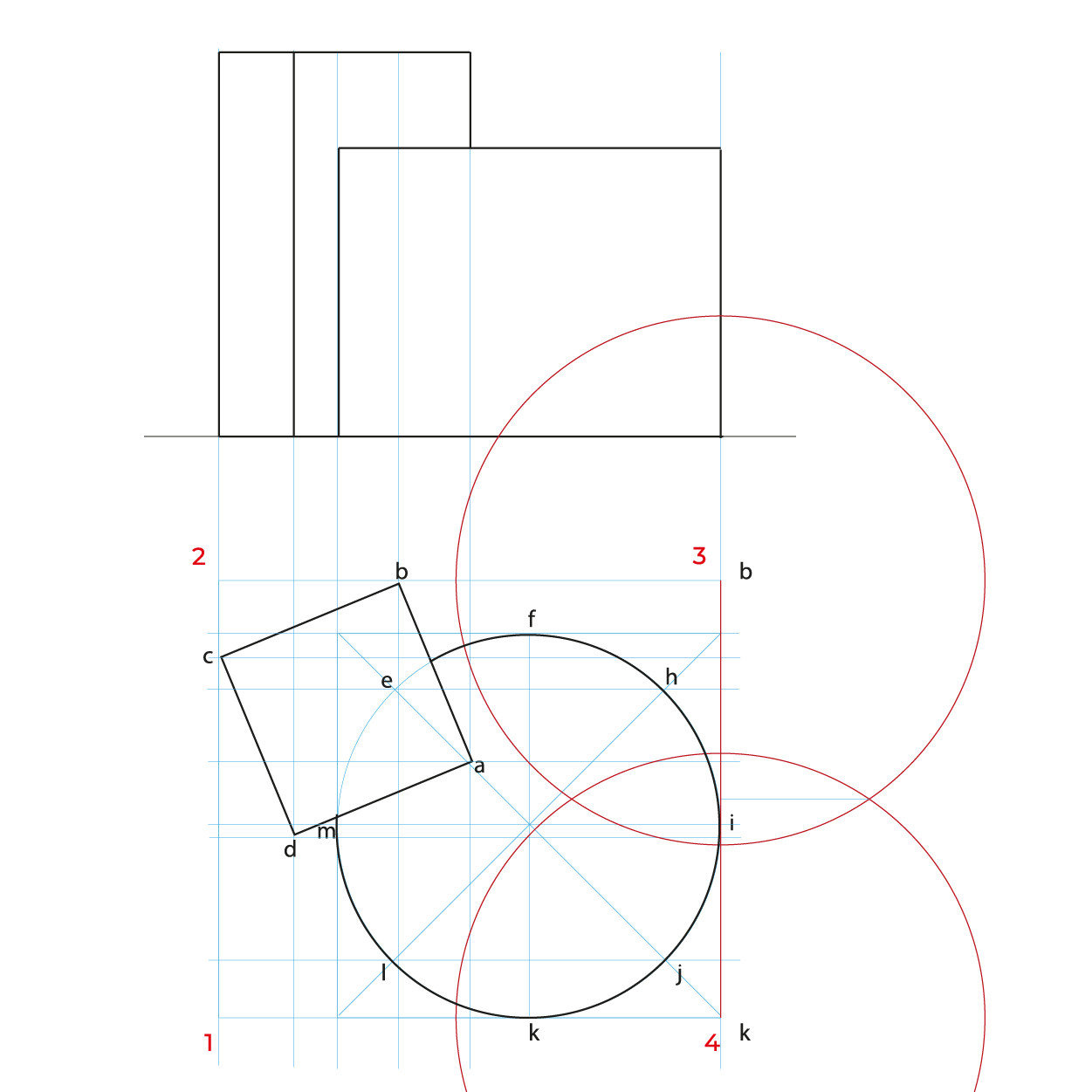
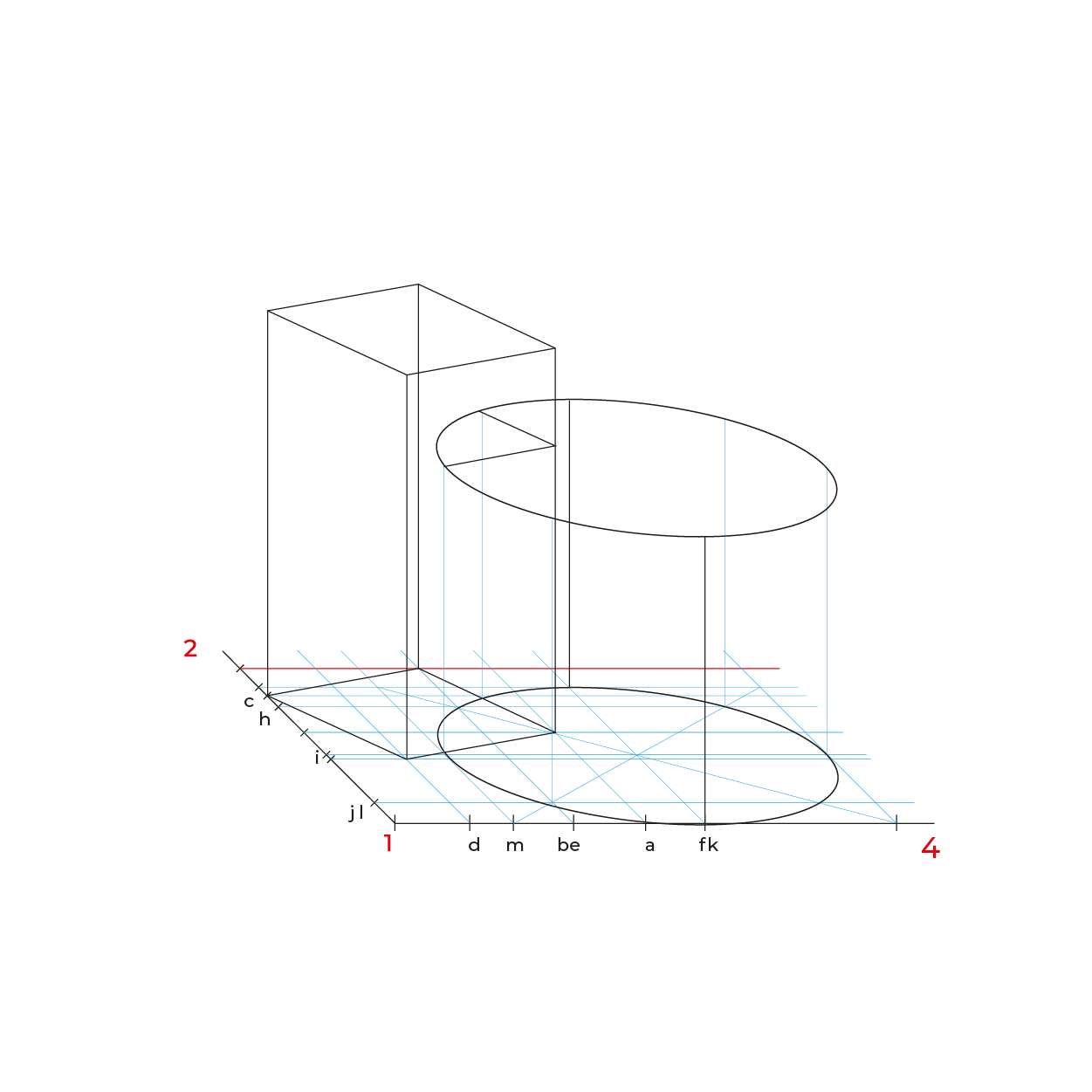
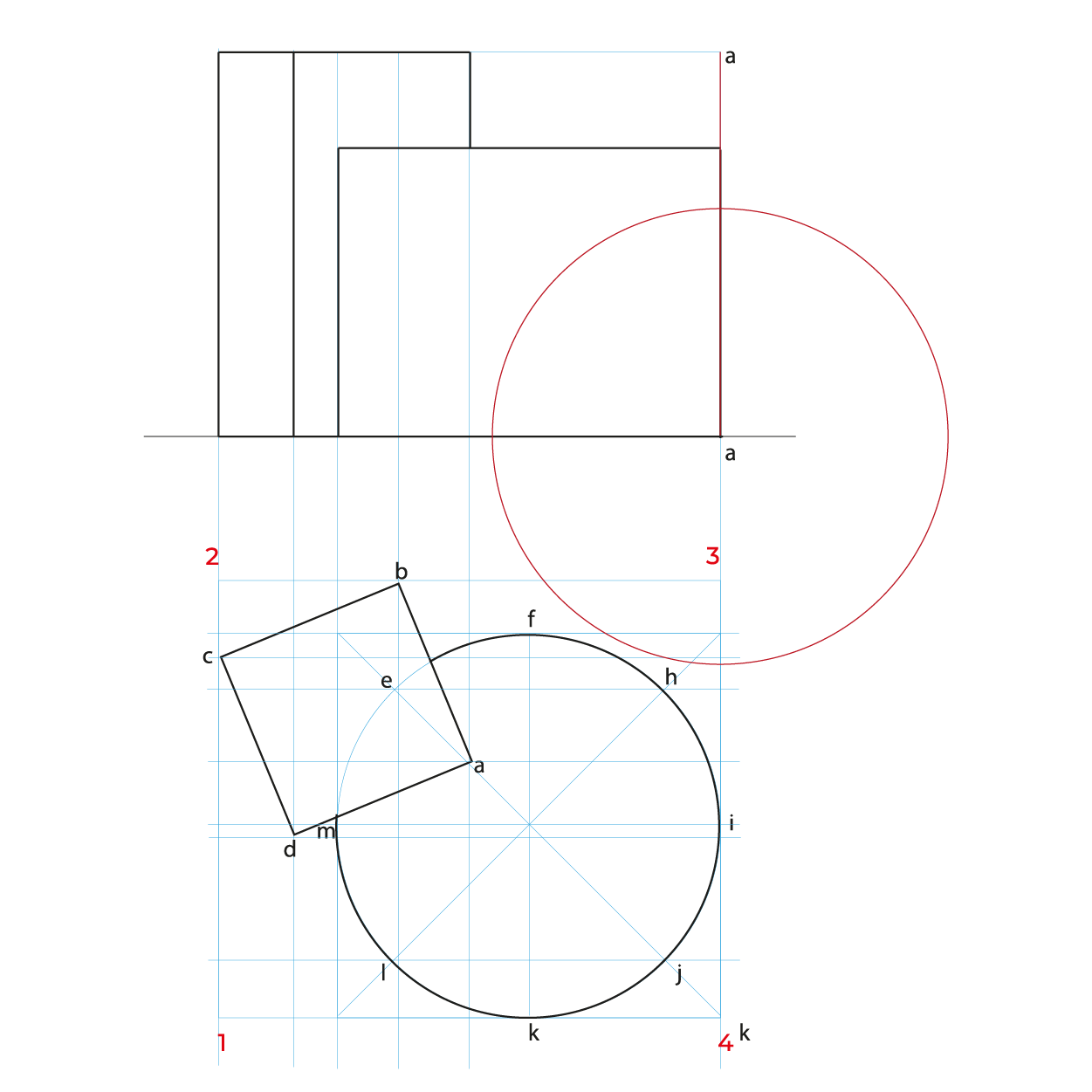
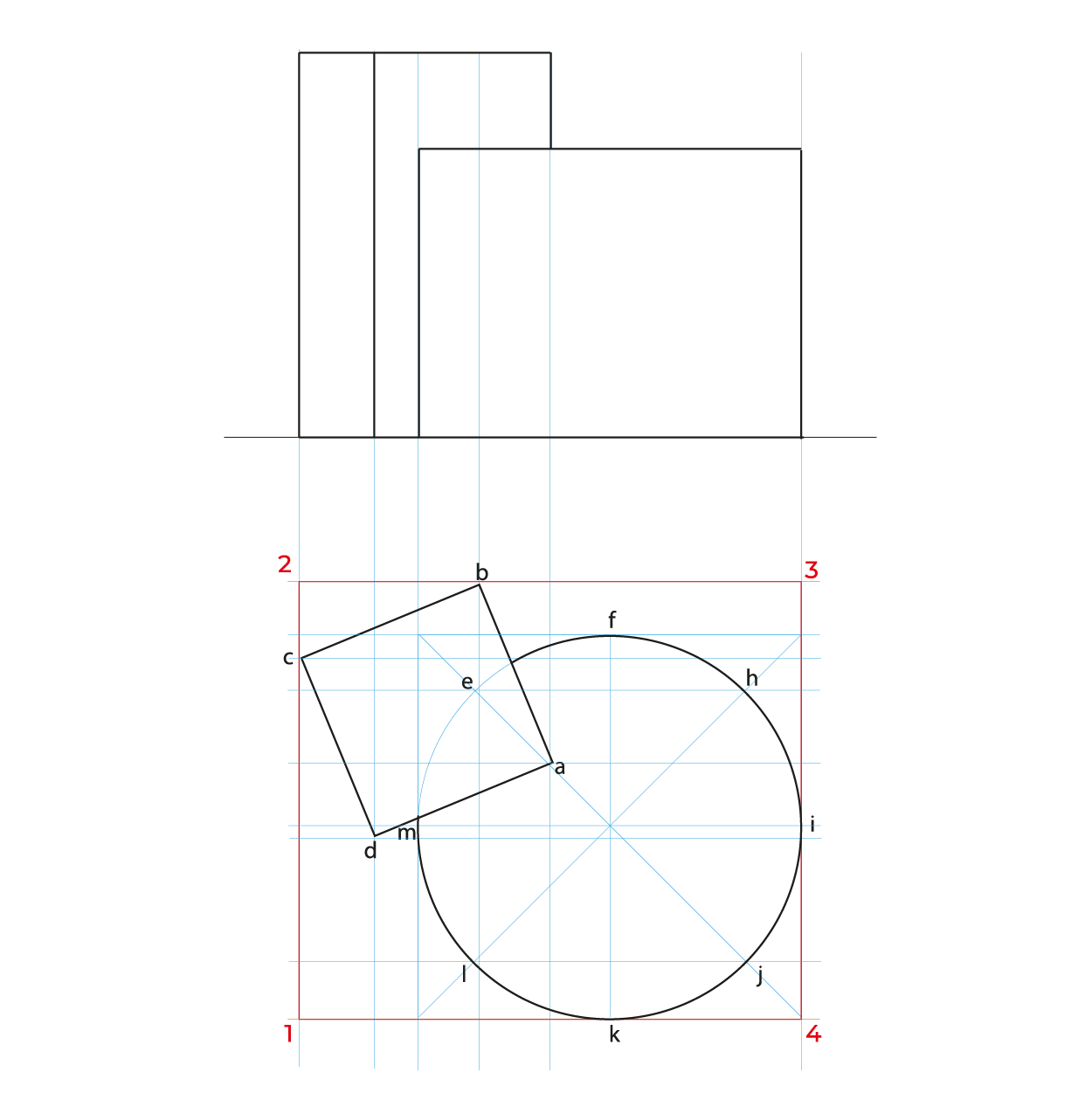
Para facilitar la construcción del subsistema no utilizaremos el triedro, construiremos un plano geometral a partir de la línea del plano del cuadro (LPC).
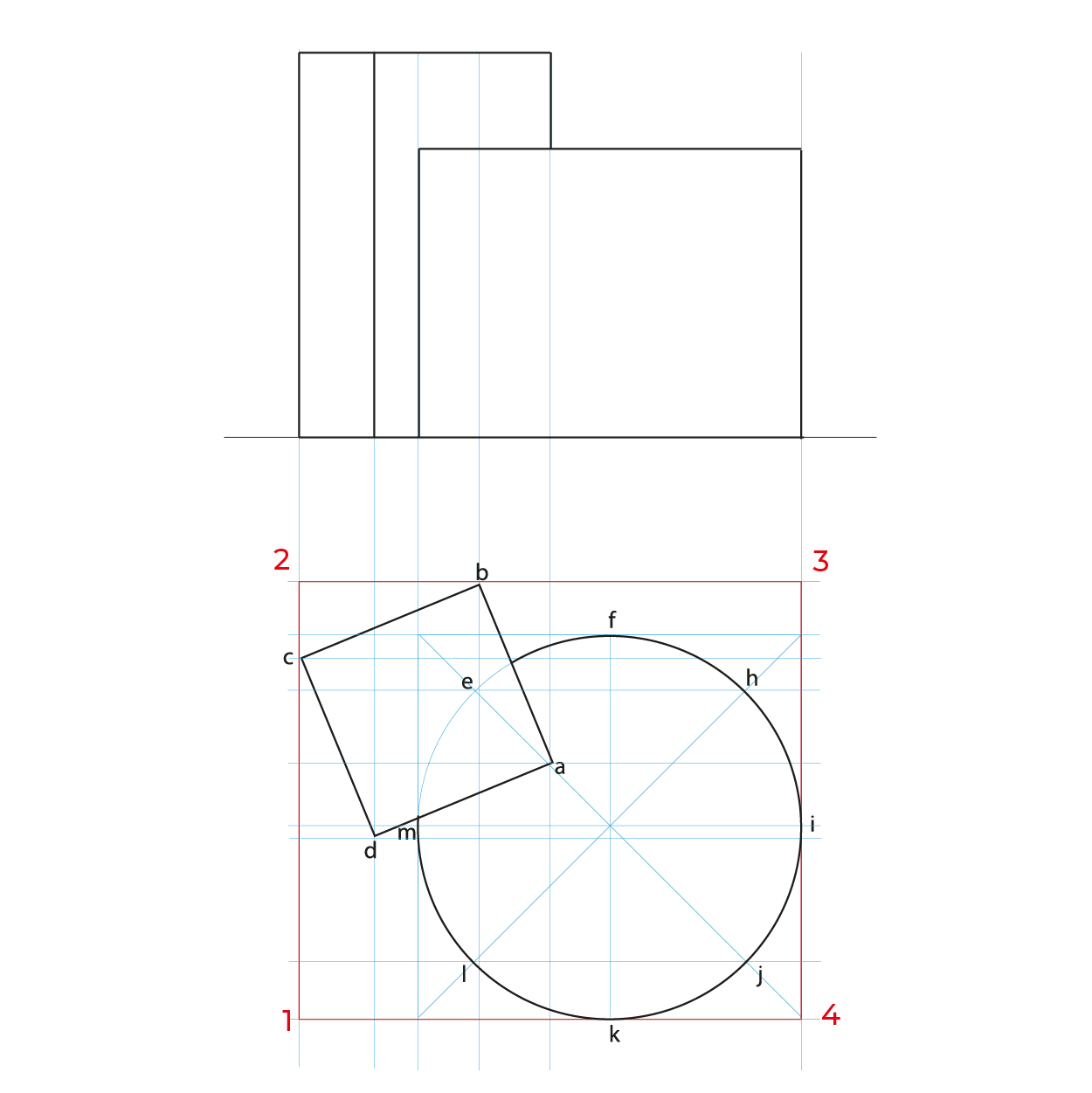
De preferencia realizar un semi-encaje en la vista superior considerando los puntos extremos, esto nos permitirá vaciar de manera correcta la información, sin equivocaciones.
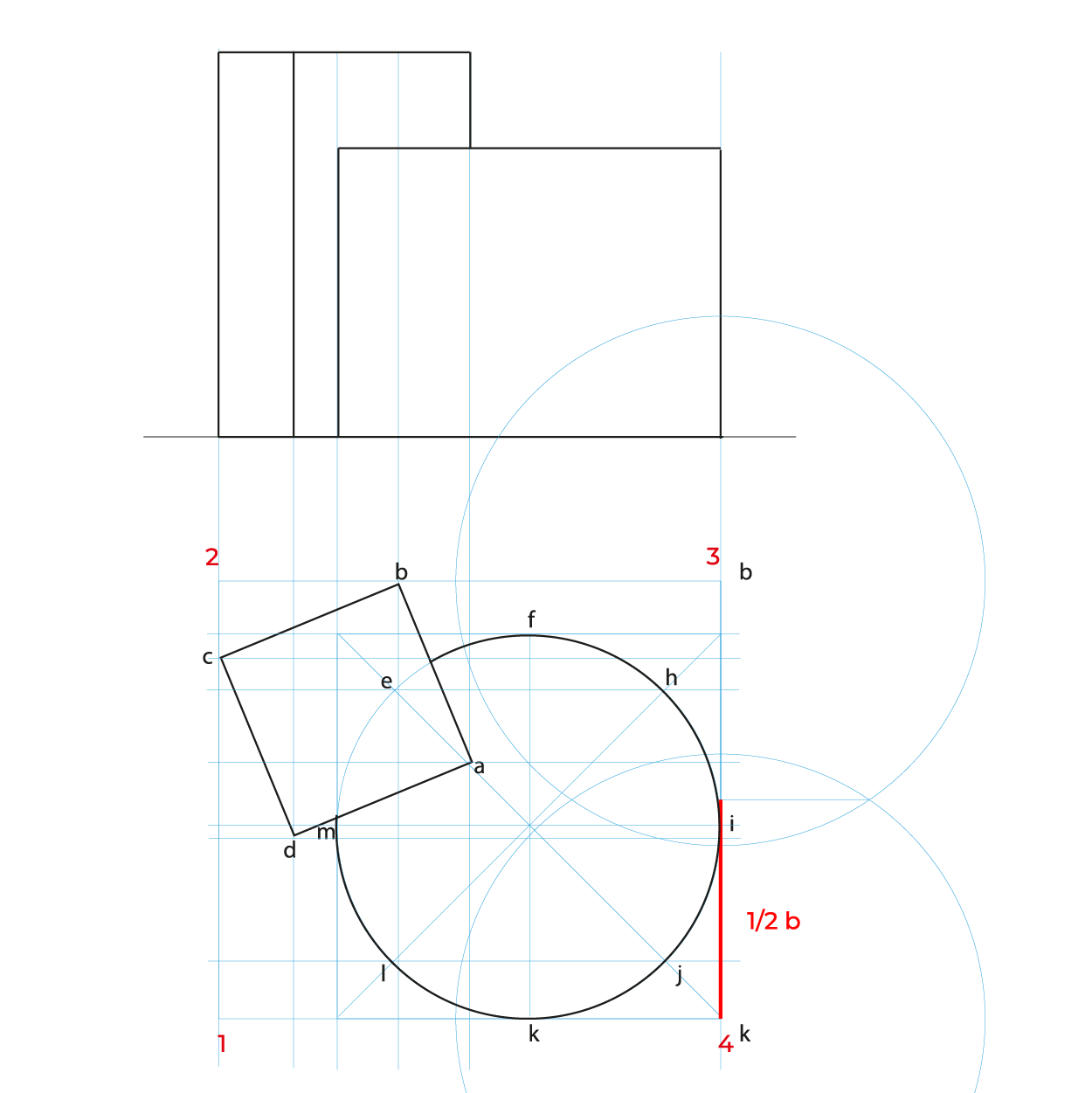
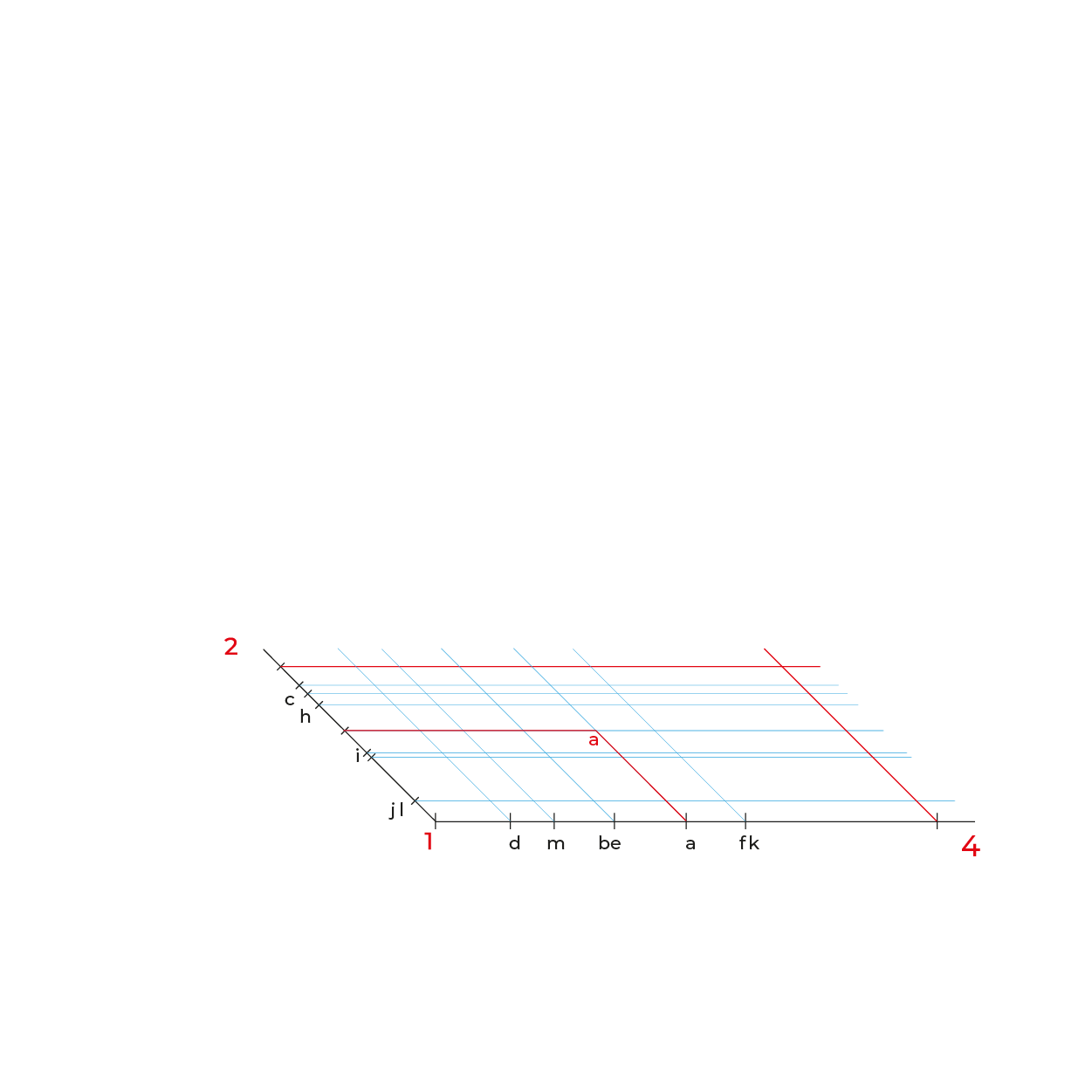
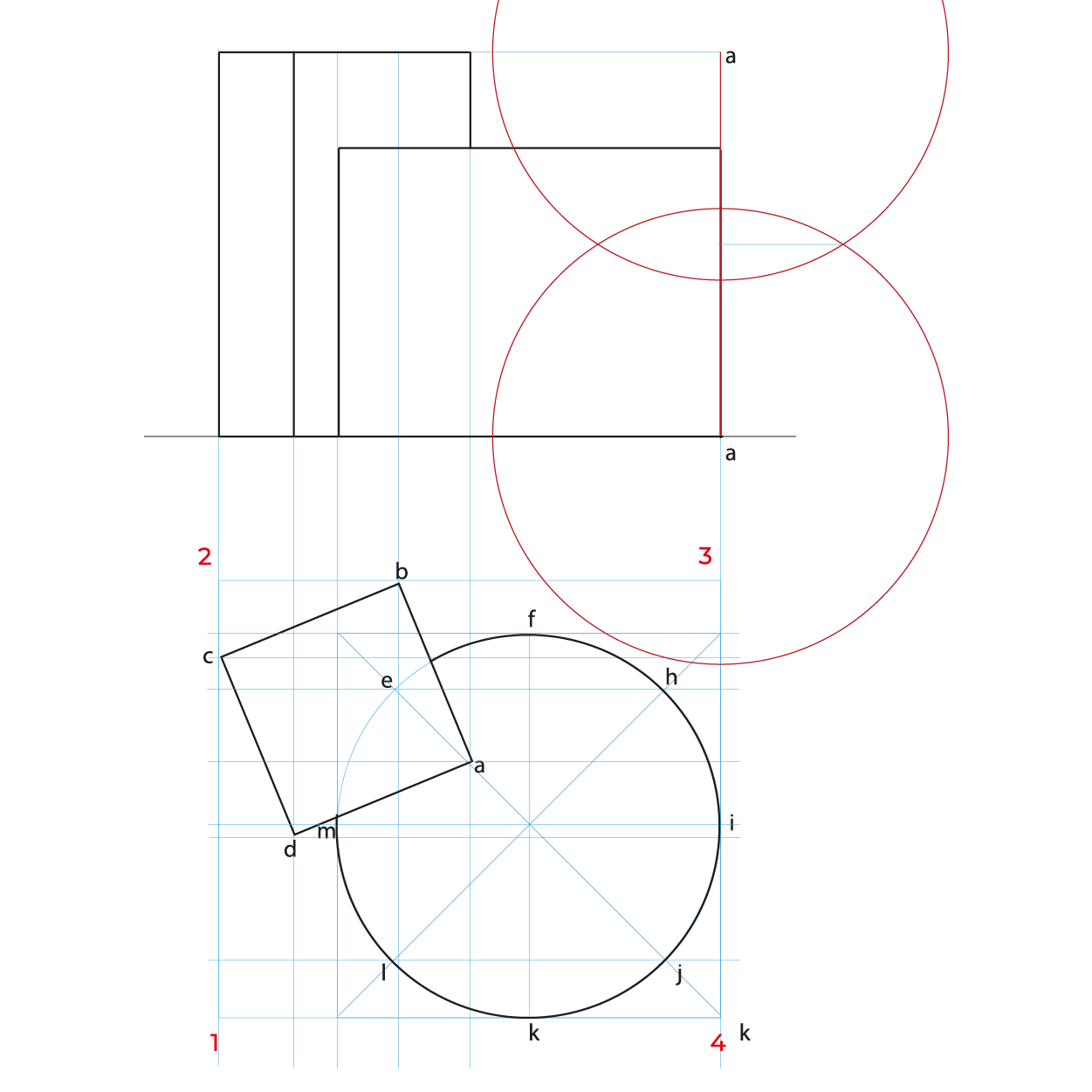
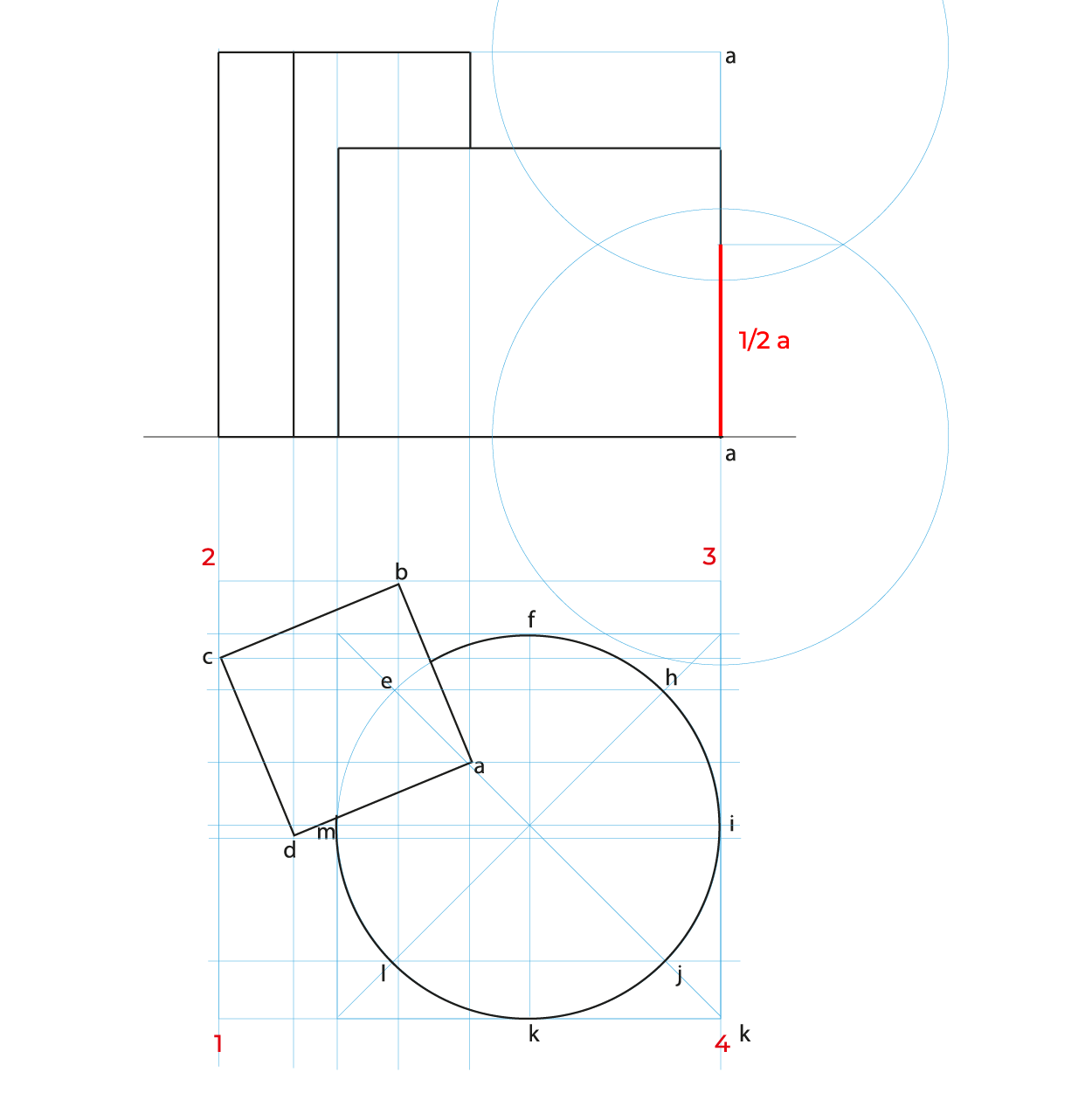
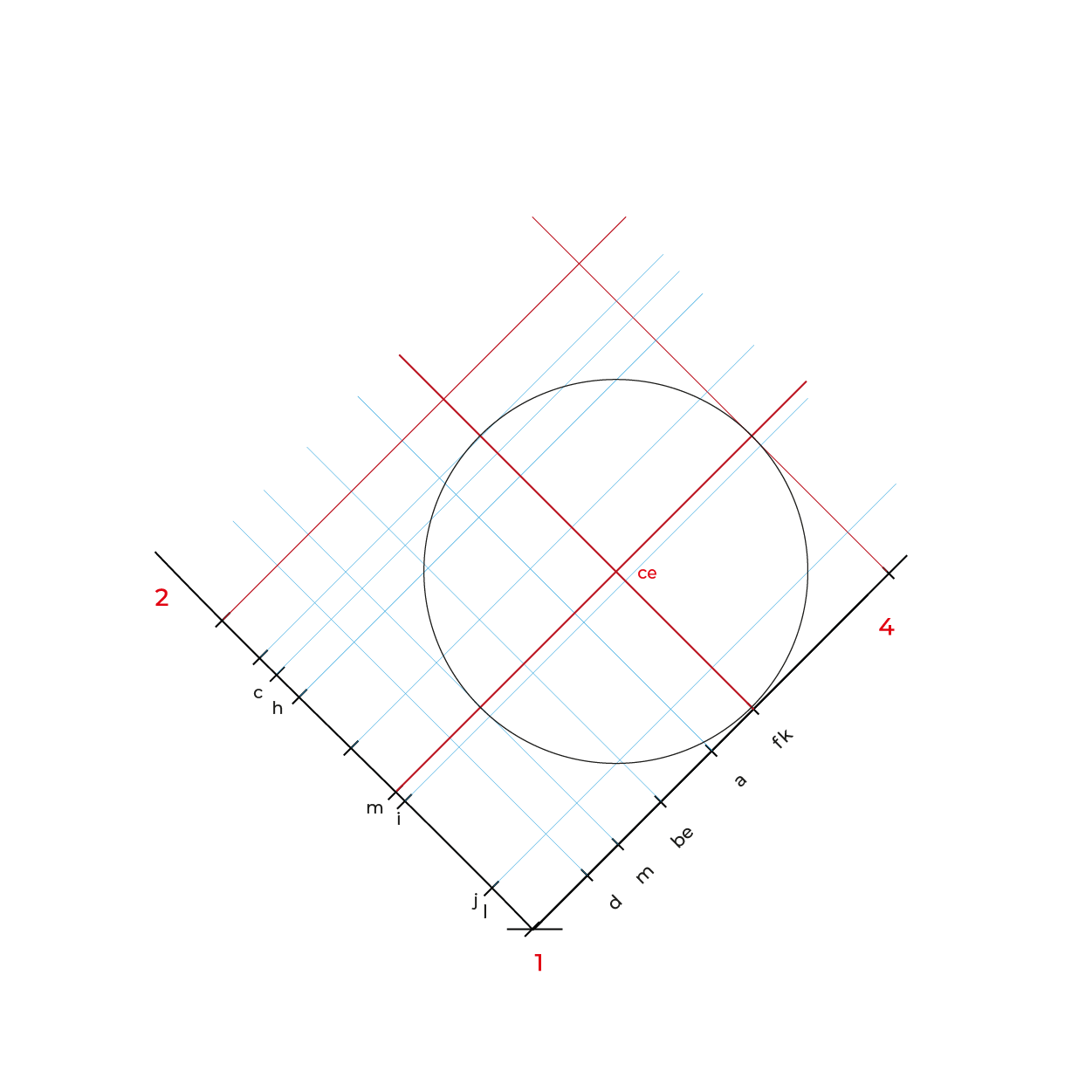
En este método es necesario hacer reducciones de manera independiente de las profundidades a ½, se puede utilizar el método revisado en los subsistemas anteriores o realizar el que se describe en este apunte.

Reducciones:

Paso 1

De acuerdo al segmento a dividir, en este caso k - b, trazaremos sobre uno de los extremos con el compás un arco que tenga un radio mayor a la mitad del segmento.

Paso 2

Con esa misma abertura utilizada, trazaremos otro arco en el extremo contrario, no es necesario trazar todas las circunferencias, lo único que necesitamos es indentificar la intersección de estos dos arcos.

Paso 3

Trazamos una línea perpendicular al segmento para llevar la intersección de los arcos a esa línea que estamos dividiendo.

Paso 4

Del punto de origen a la línea trazada, tenemos matemáticamente la mitad del segmento a dividir. Este proceso se repite con cada uno de los puntos de la figura.

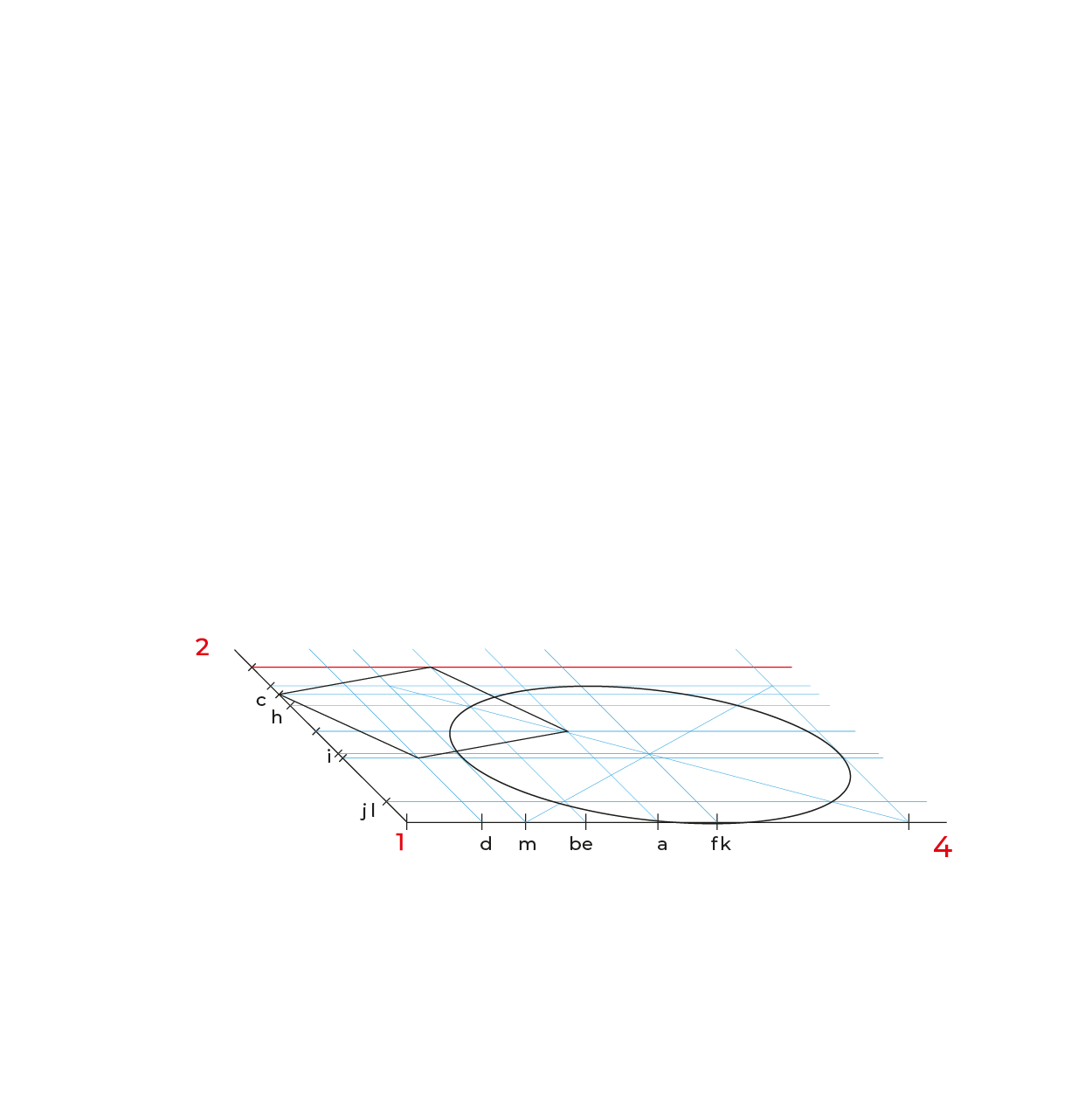
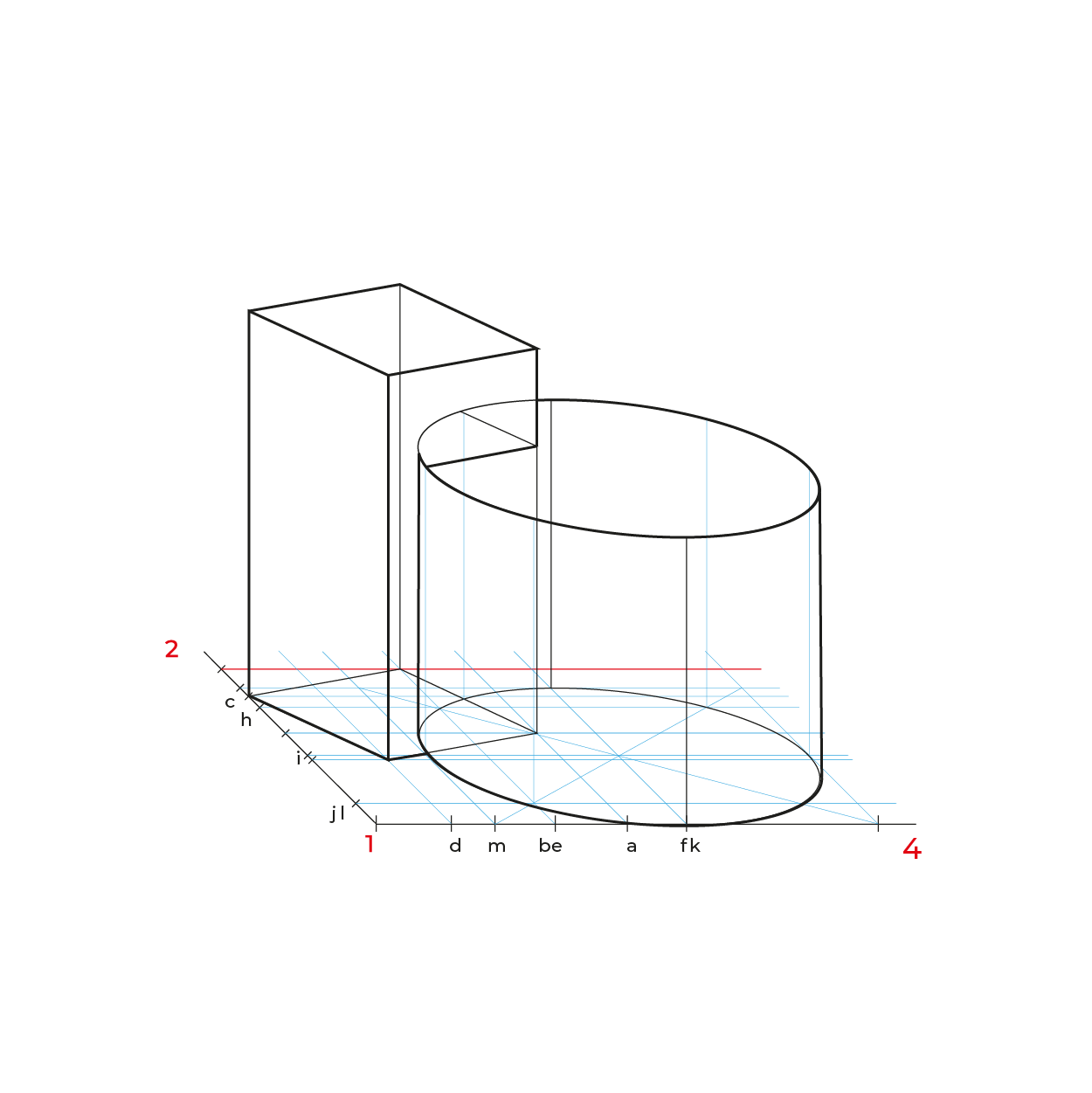
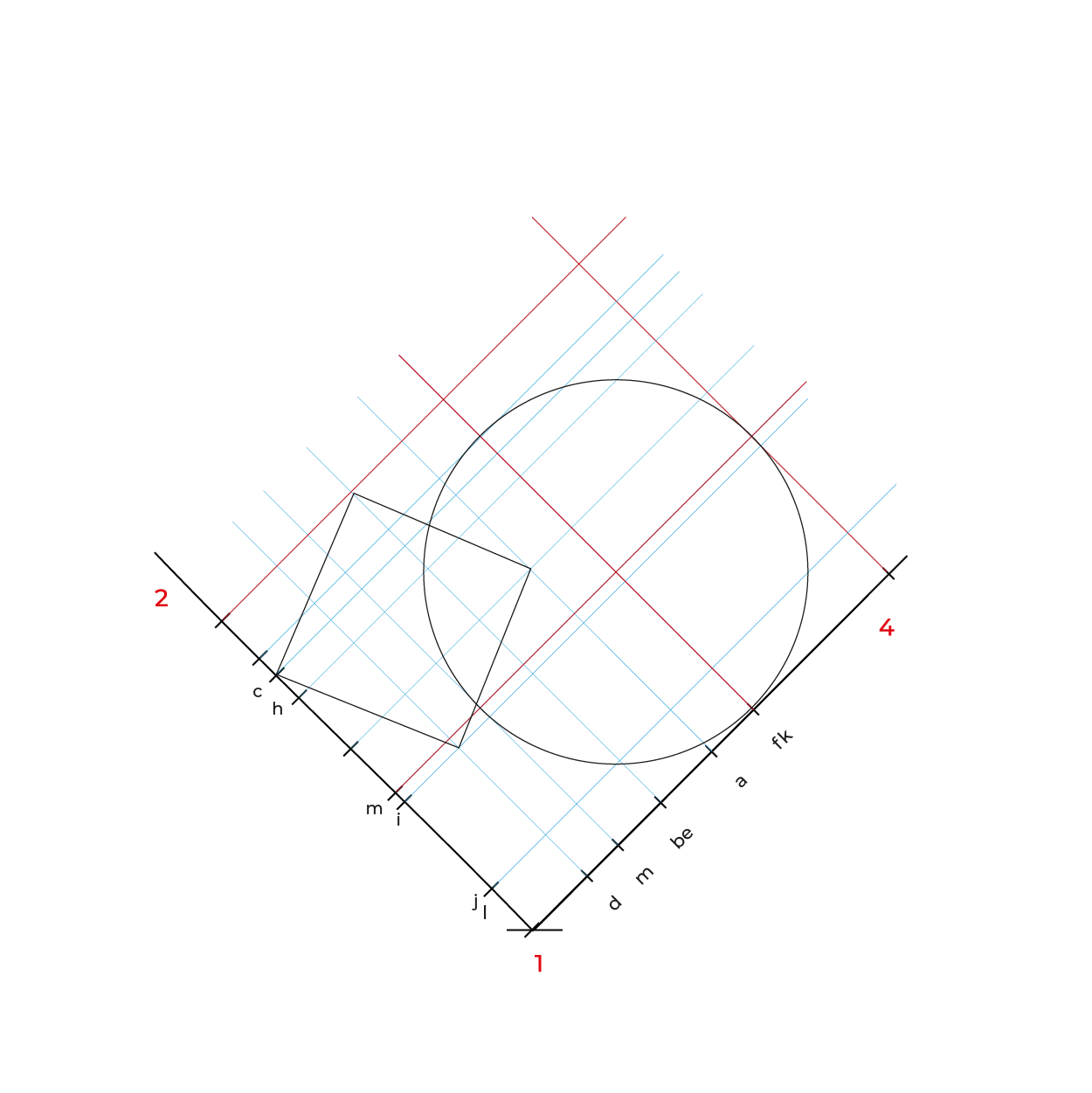
En el caso de la circunferencia de la base del cilindro, solo es necesario reducir la distancia de K-J, ya que es la misma de H-F y la mitad de KF es I, esto para evitar reducir tantos puntos.

El proceso

Paso 1

De preferencia trazar un semiencage con los puntos extremos, numerando de esta forma (al igual que en todos los métodos de coordenadas) y realizar de manera previa las reducciones en altura a 1/2.

Paso 2

Se coloca la LPC, en este caso sobre ella colocaremos las anchuras y a partir de ella se genera un plano geometral de 135°, se construye a partir de un eje de profundidades de 45°.

Paso 3

Vaciamos la información de anchuras de 1 a 4, y de profundidades, de 1 a 2.

Paso 4

Con líneas paralelas y perpendiculares a los ejes unimos 2 y 4, esto nos delimitará el espacio a utilizar, ninguno de los puntos de nuestra figura deberá salir de este espacio.

Paso 5

A partir de los puntos en anchuras trazar líneas guía paralelas al eje contrario, del lado contrario hacer lo mismo, a partir de los puntos en profundidades trazar líneas guía paralelas al eje contrario.

Paso 6

Localizar por coordenadas la intersección de los puntos, en este caso el punto a.

Paso 7

Ubicar sobre el piso los puntos que corresponden al objeto a construir

Paso 8

Levantar los puntos que tengan altura por medio de líneas verticales, perpendiculares a la LPC y colocar la altura correspondiente de la montea.

Paso 9

Unir los puntos del objeto con sus correspondientes para generar la representación tridimensional.

Paso 10

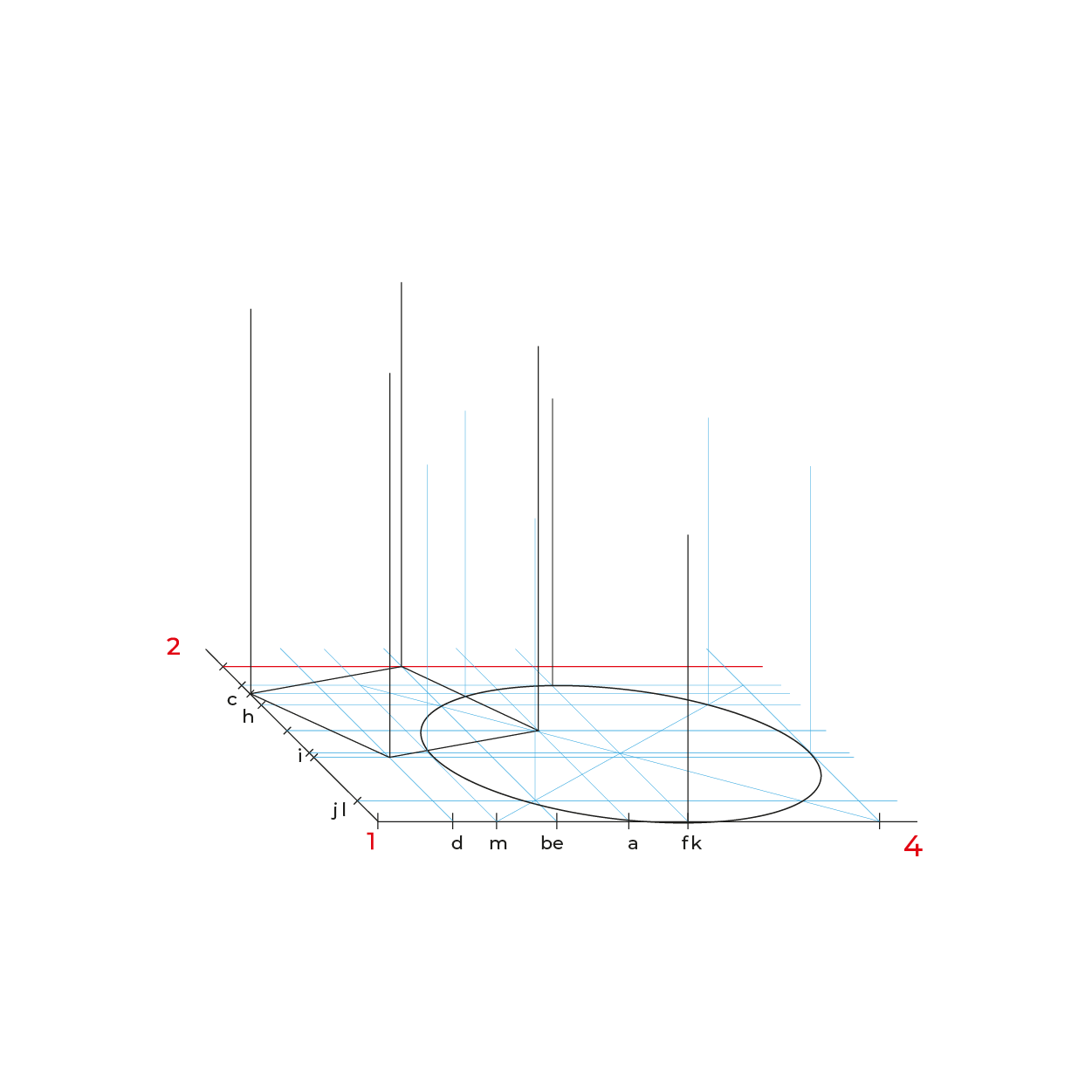
Dar calidad de línea, solo trazando de manera fuerte las aristas que se ven del objeto

A continuación puedes revisar el siguiente video, en él se explica y se realiza el método desglosado anteriormente, si lo deseas, también descargar los pasos anteriores del apunte PDF Subsistema Caballera

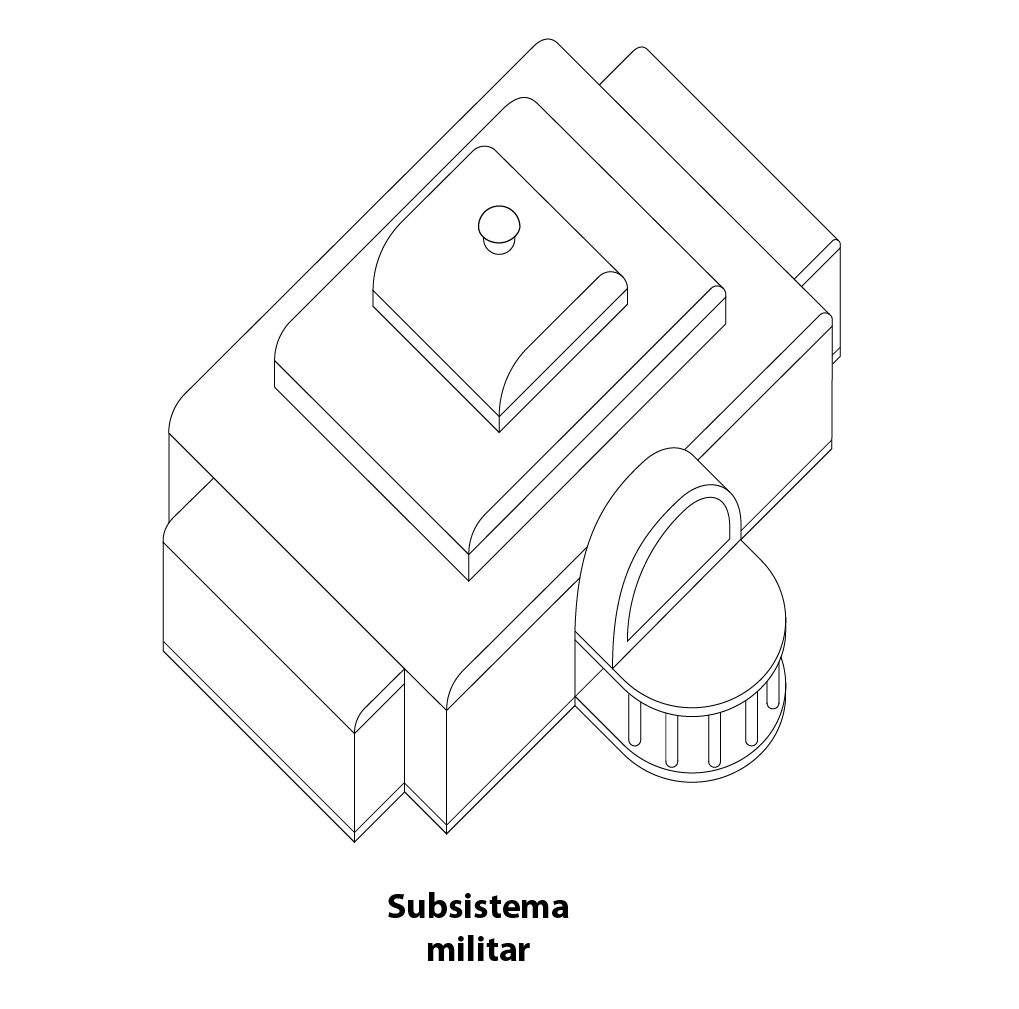
Militar

El subsistema militar recibe su nombre debido a su utilización por parte de los ingenieros militares, en especial en la representación de fortificaciones. Este tipo de representación es especialmente útil en la representación de edificios. En la actualidad, quienes más utilizan este tipo de representación son las agencias inmobiliarias y empresas de construcción a la hora de mostrar los planos a los clientes. Su principal ventaja radica en que las dimensiones de la planta no se modifican. Por este motivo es muy útil para hacerse una idea de las dimensiones de objetos y estancias.

Guarda mucha similitud con el subsistema caballera, pero con la particularidad de que el la reducción se aplica a las alturas, y no a las profundidades.

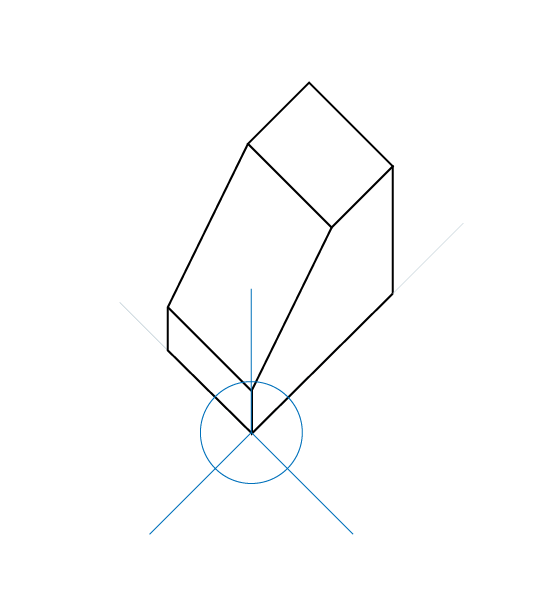
El plano del cuadro conformado por los ejes X y Y forman un ángulo de 90º.

Compensación en las magnitudes:
Al tener variantes en diversos ángulos, existen diversas escalas. Generalmente las alturas se reducen a la mitad. 1:1/2:1

Planta sin distorsión.
Vista cenital acentuada.
Apta para objetos que no tienen ángulos rectos.
Especialmente adecuada para objetos complejos y edificios.
Es muy usada en las perspectivas de arquitectura e ingeniería civil.

Ángulos que utilizaremos para construcción del plano geometral

Ángulos empleados para la construcción del subsistema militar

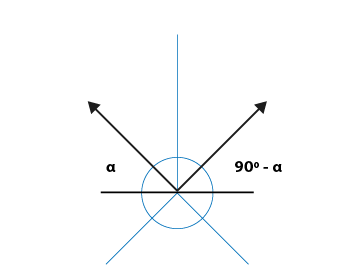
Método por coordenadas

Consideraciones:

Montea biplanar, no es necesaria la vista auxiliar
Para facilitar la construcción del subsistema no utilizaremos el triedro, construiremos un plano geometral a partir de la línea del plano del cuadro (LPC).
De preferencia realizar un semi-encaje en la vista superior considerando los puntos extremos, esto nos permitirá vaciar de manera correcta la información, sin equivocaciones.
En este método es necesario hacer reducciones de manera independiente de las profundidades a ½.

Reducciones:

Paso 1

De acuerdo al segmento a dividir, en este caso a - a, trazaremos sobre uno de los extremos con el compás un arco que tenga un radio mayor a la mitad del segmento.

Paso 2

Paso 3

Trazamos una línea perpendicular al segmento para llevar la intersección. Del punto de origen a la línea trazada, tenemos matemáticamente la mitad del segmento a dividir. Este proceso se repite con cada una de las alturas

El proceso

Paso 1

De preferencia trazar un semiencage con los puntos extremos, numerando de esta forma (al igual que en todos los métodos de coordenadas) y realizar de manera previa las reducciones en altura a 1/2.

Paso 2

Se coloca la LPC y a partir de ella se genera un plano geometral de 90°, no importa la inclinación de los ejes que lo construyen, puede ser 45° y 45°, 30° y 60°, esto dependerá de buscar la mejor composición y la evidencia de las intersecciones.

Paso 3

Vaciamos la información de anchuras de 1 a 4, y de profundidades, de 1 a 2.

Paso 4

Con líneas paralelas y perpendiculares a los ejes unimos 2 y 4, esto nos delimitará el espacio a utilizar, ninguno de los puntos de nuestra figura deberá salir de este espacio.

Paso 5

Paso 6

Localizar por coordenadas la intersección de los puntos, en este caso el punto c a partir de f y m, ya que esto nos permitirá trazar el círculo de la base del prisma con compás a partir de su centro y tener que buscar cada uno de los 8 puntos auxiliares.