Subsistema trimétrico

Definición

La palabra trimétrico proviene del latín tri que significa “tres” y del griego metron que significa “medida”. Por lo que una representación trimétrica consiste en la representación gráfica de un objeto tridimensional de manera bidimensional en la cual los tres ejes que constituyen el plano de proyección forman tres ángulos de amplitud diferente.

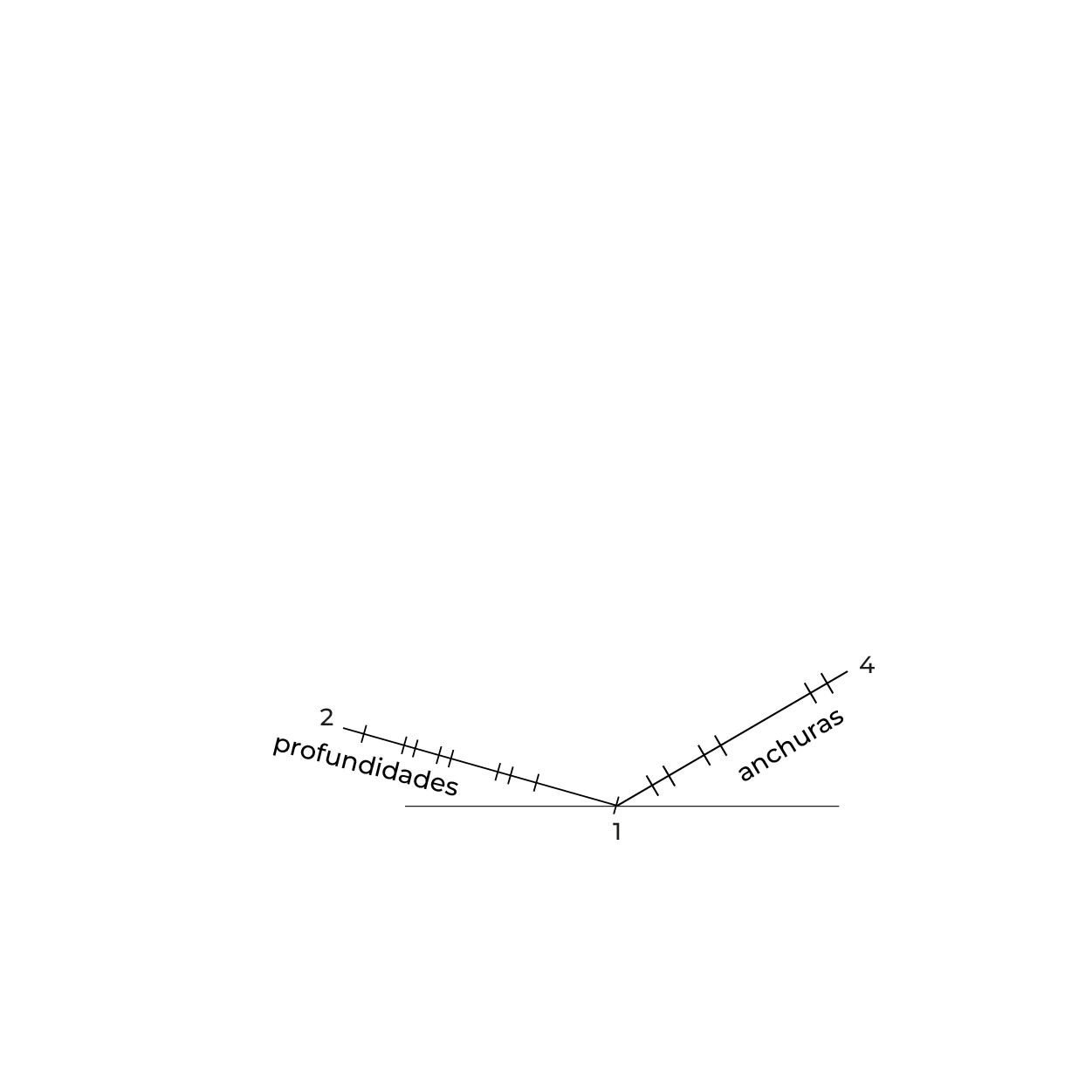
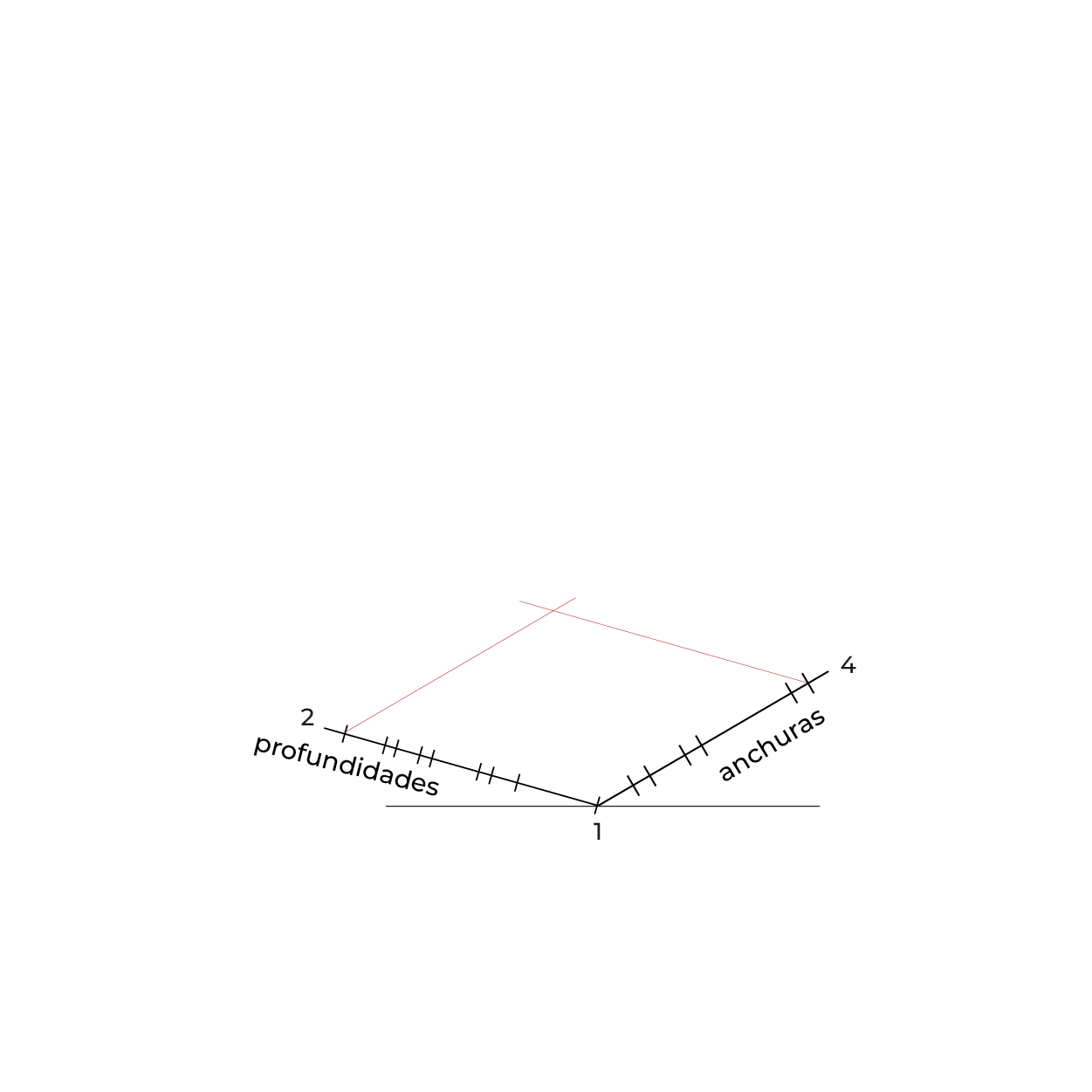
En éste tipo de subsistema, las dimensiones correspondientes a cada uno de los ejes se manejan en tres escalas diferentes, es decir, existe alteración en las medidas del plano descriptivo (montea) correspondientes a las profundidades y a las anchuras, siendo las alturas las únicas que conservan su magnitud original. Con estos ajustes ocurre una ligera deformación en la vista del objeto, misma que refleja una disminución aparente en su tamaño, la cual resulta proporcional a la distancia que se percibe por el ojo humano.

Como ocurre en el subsistema dimétrico, el ajuste a las profundidades se hace a ⅔ de la magnitud real del objeto en la montea, el ajuste a las anchuras a ⅚ partes de la magnitud real.

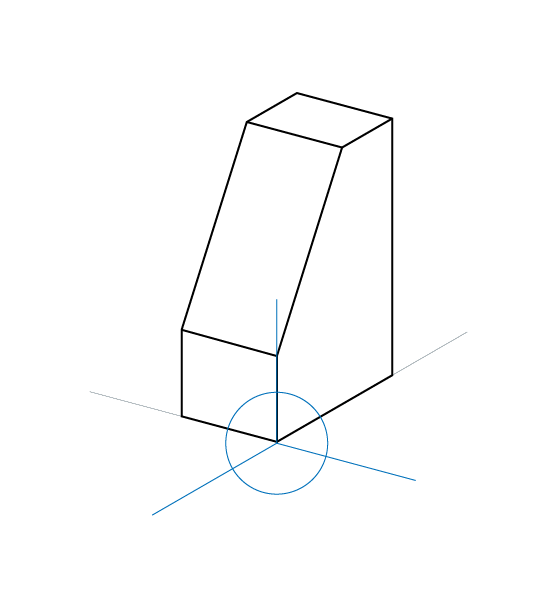
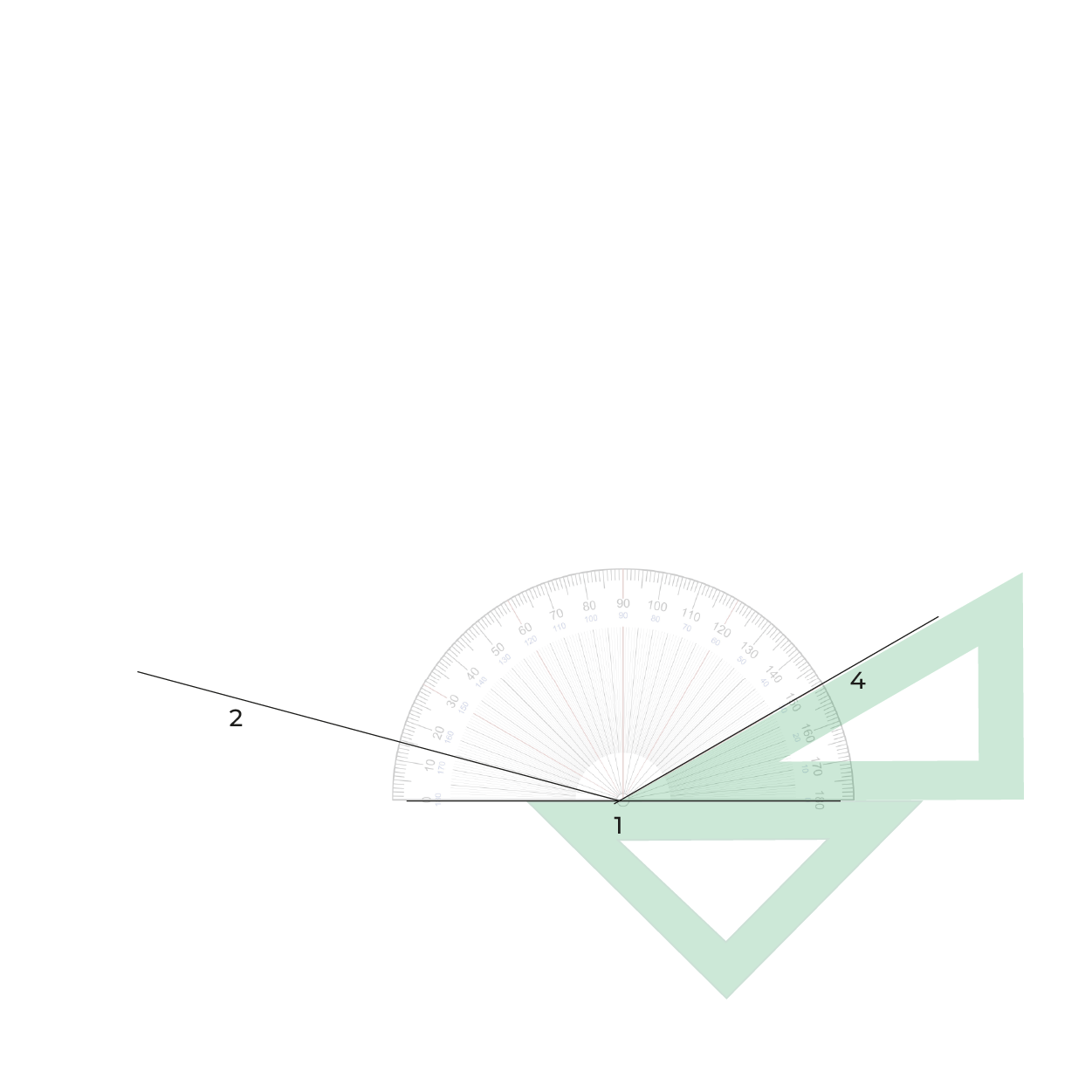
Los tres ejes que constituyen el plano de proyección, forman tres ángulos de amplitud diferente.

Compensación en las magnitudes:
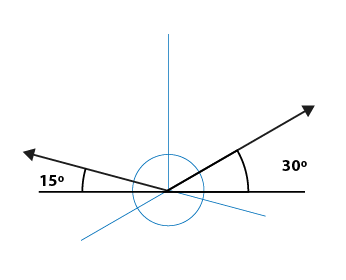
Igual que en el dimétrico existen diversas compensaciones dependiendo de los ángulos, para este caso, las anchuras se redujeron a 5/6 partes y las profundidades a 2/3 partes. 5/6:1:2/3

Apta para objetos con poca profundidad.
Claridad visual.

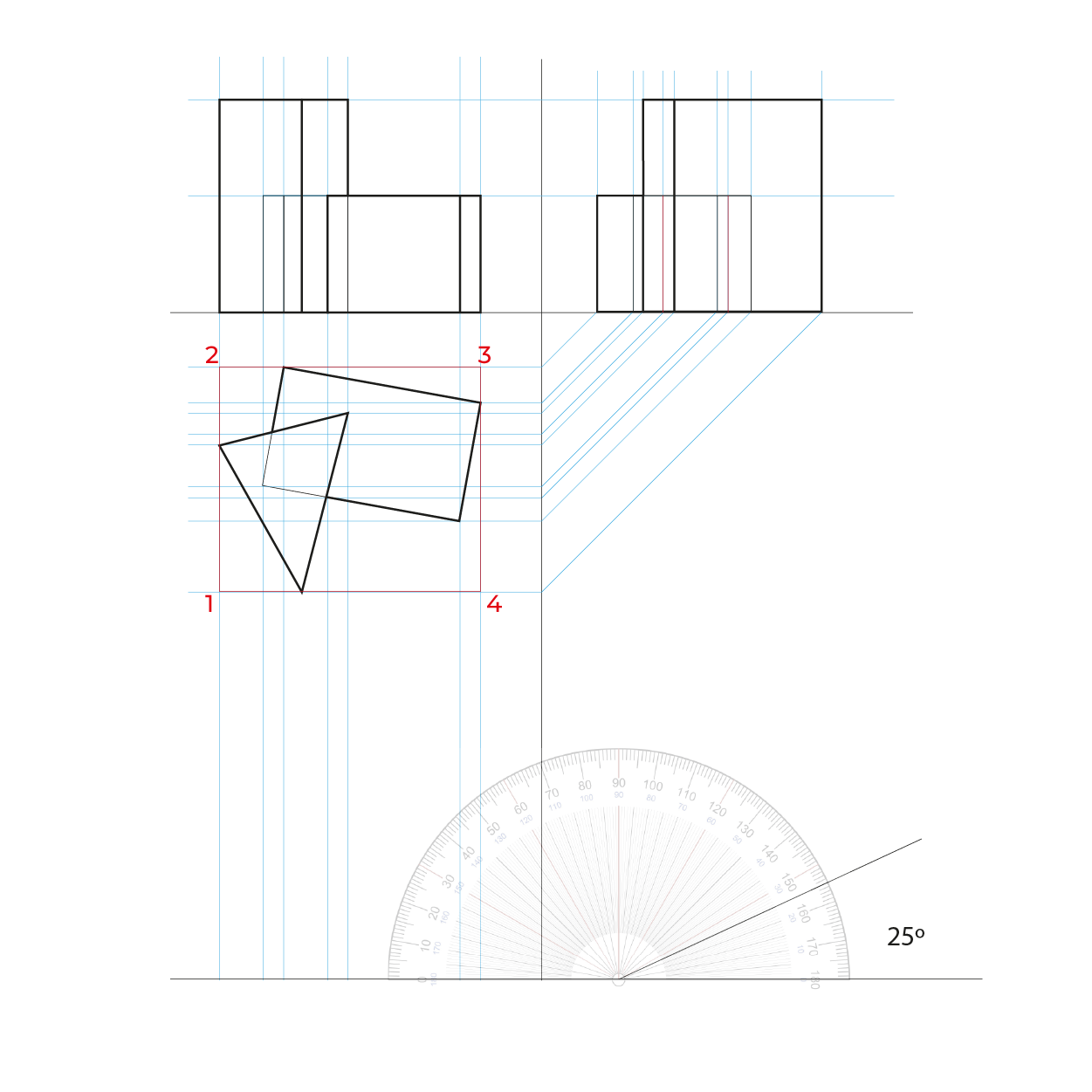
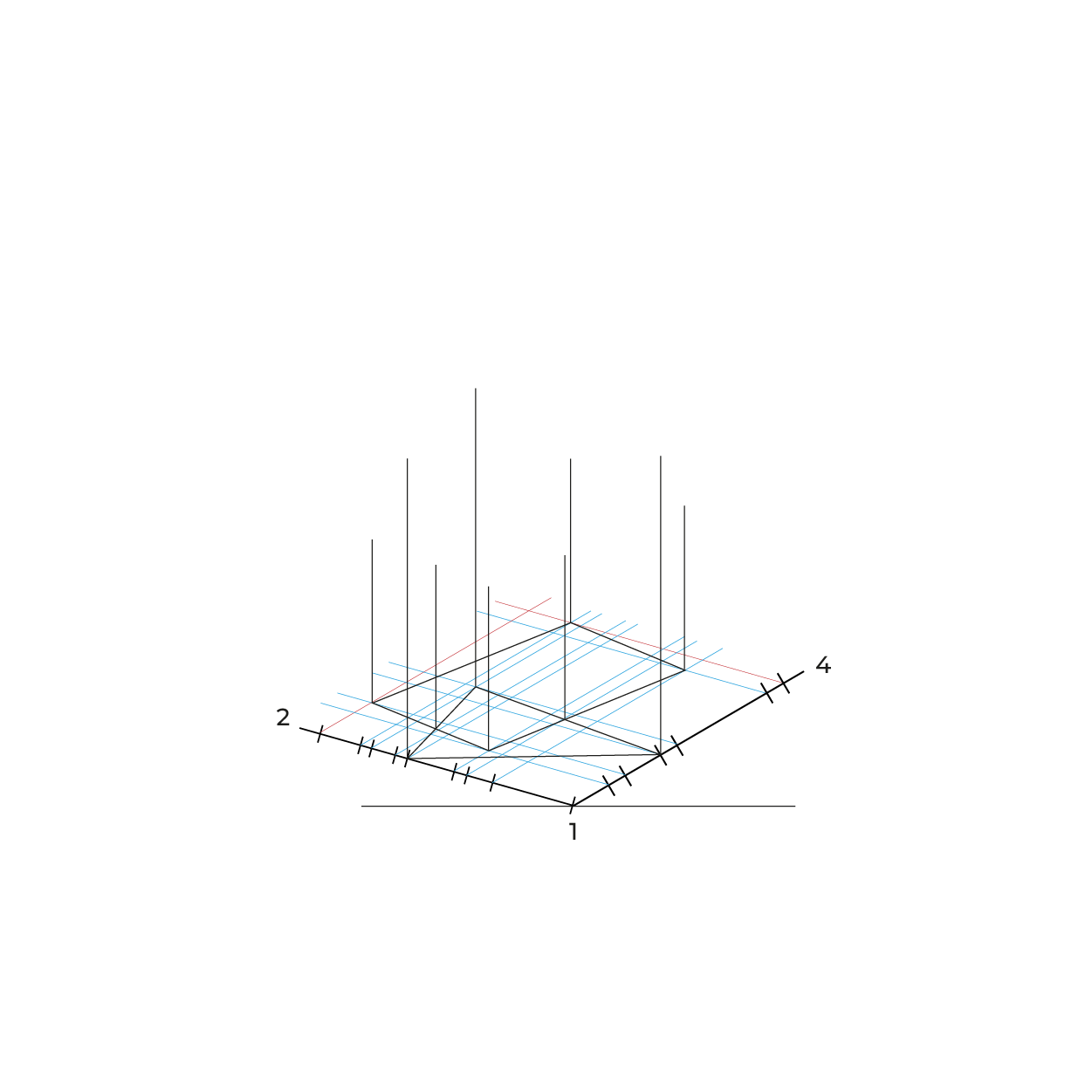
Ángulos que utilizaremos para construcción del plano geometral

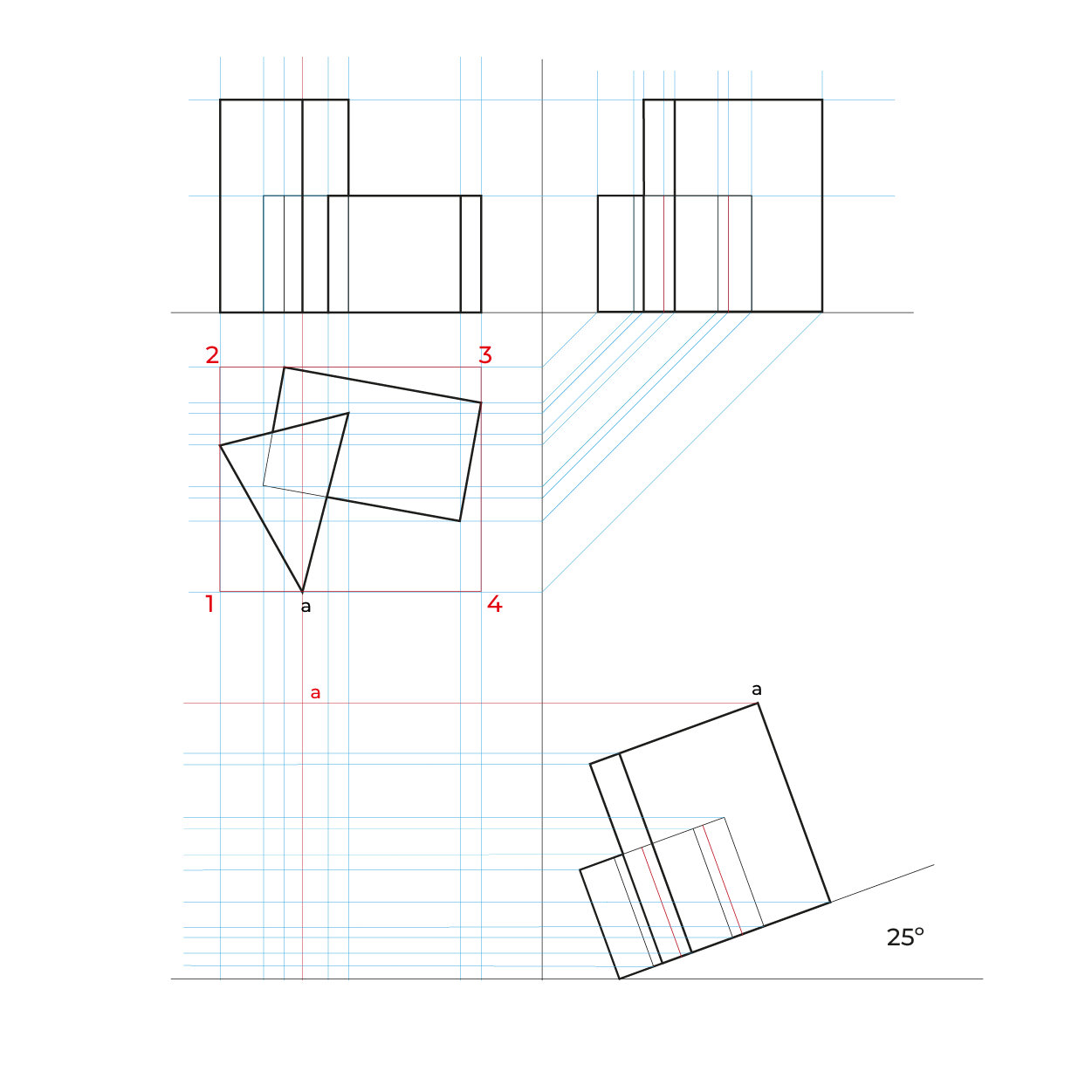
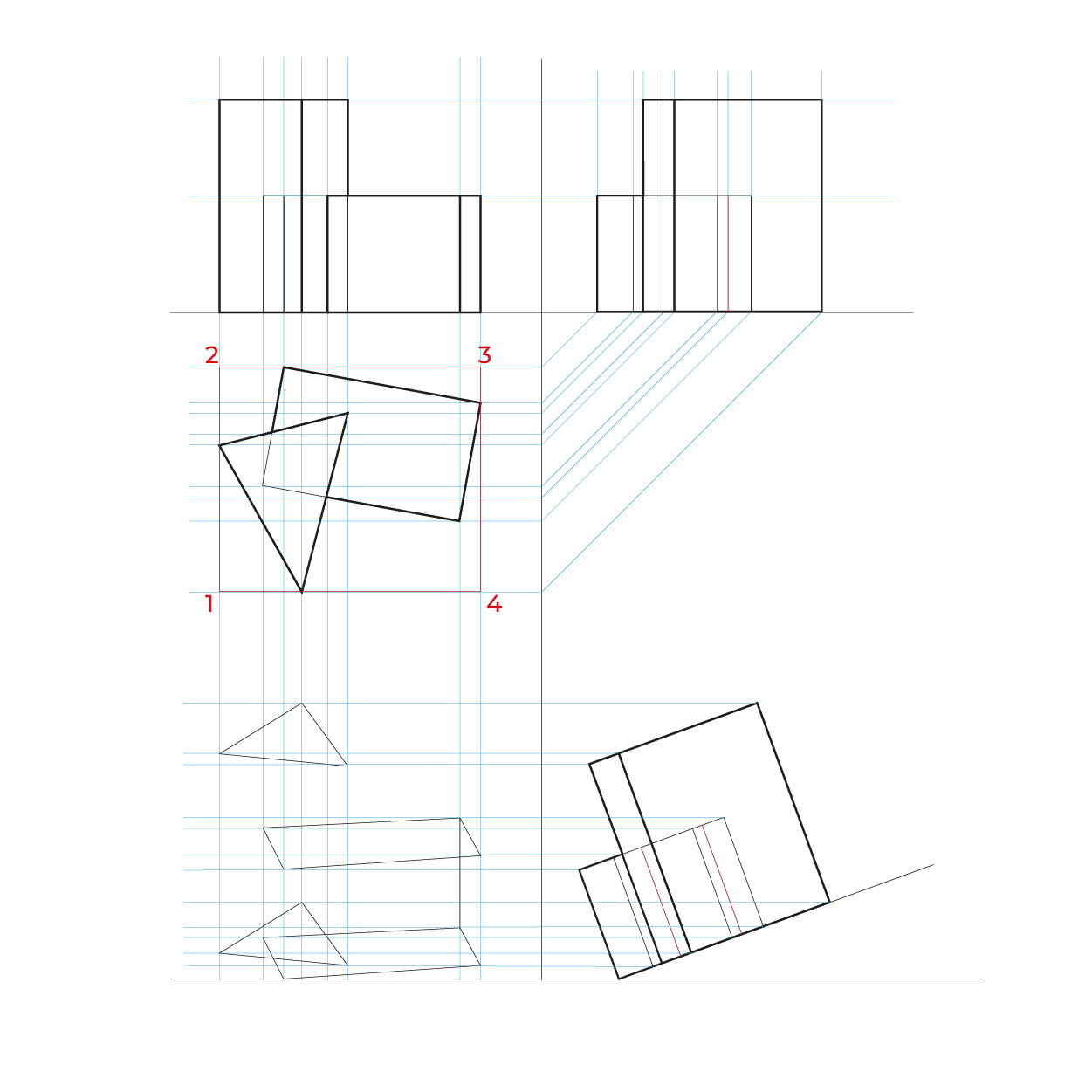
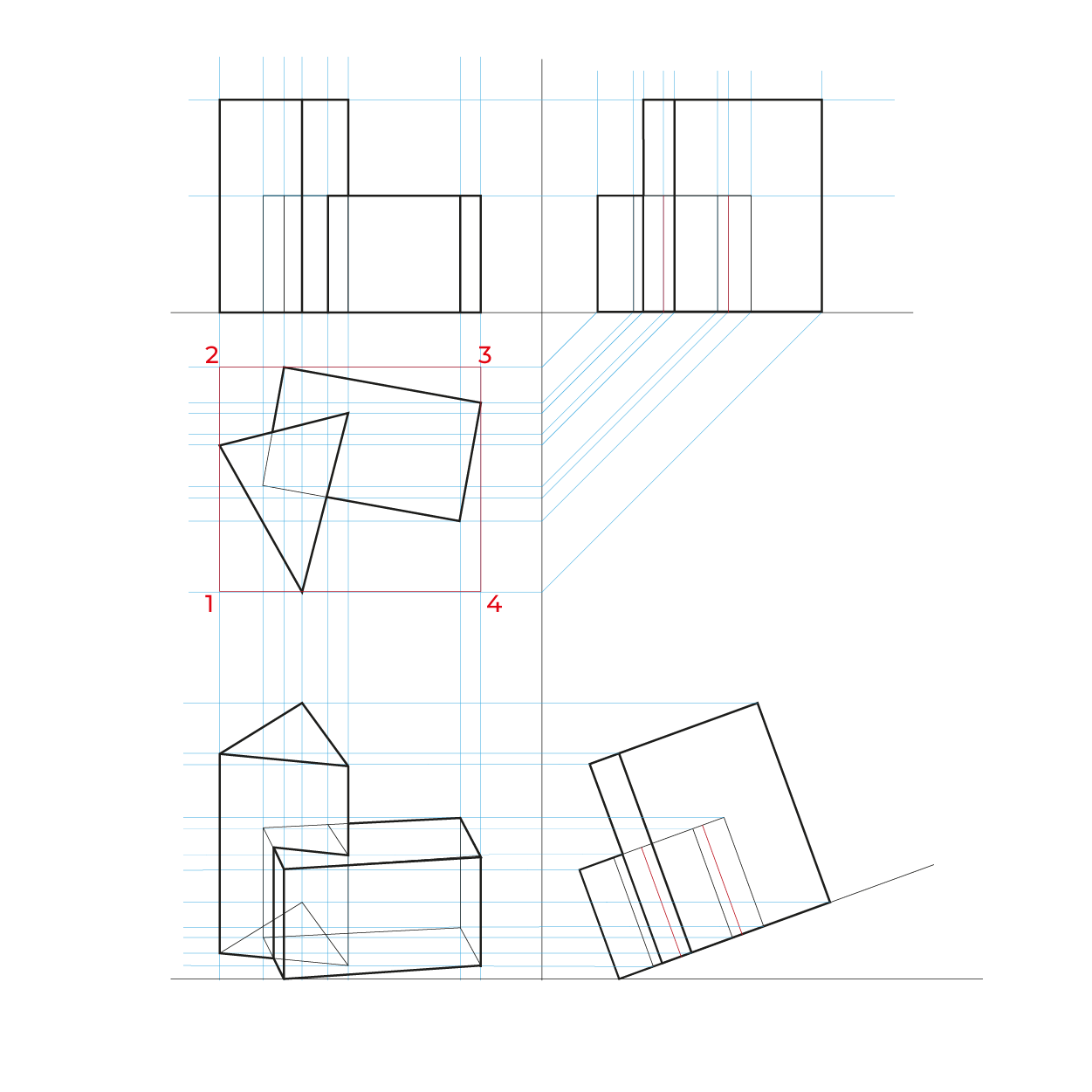
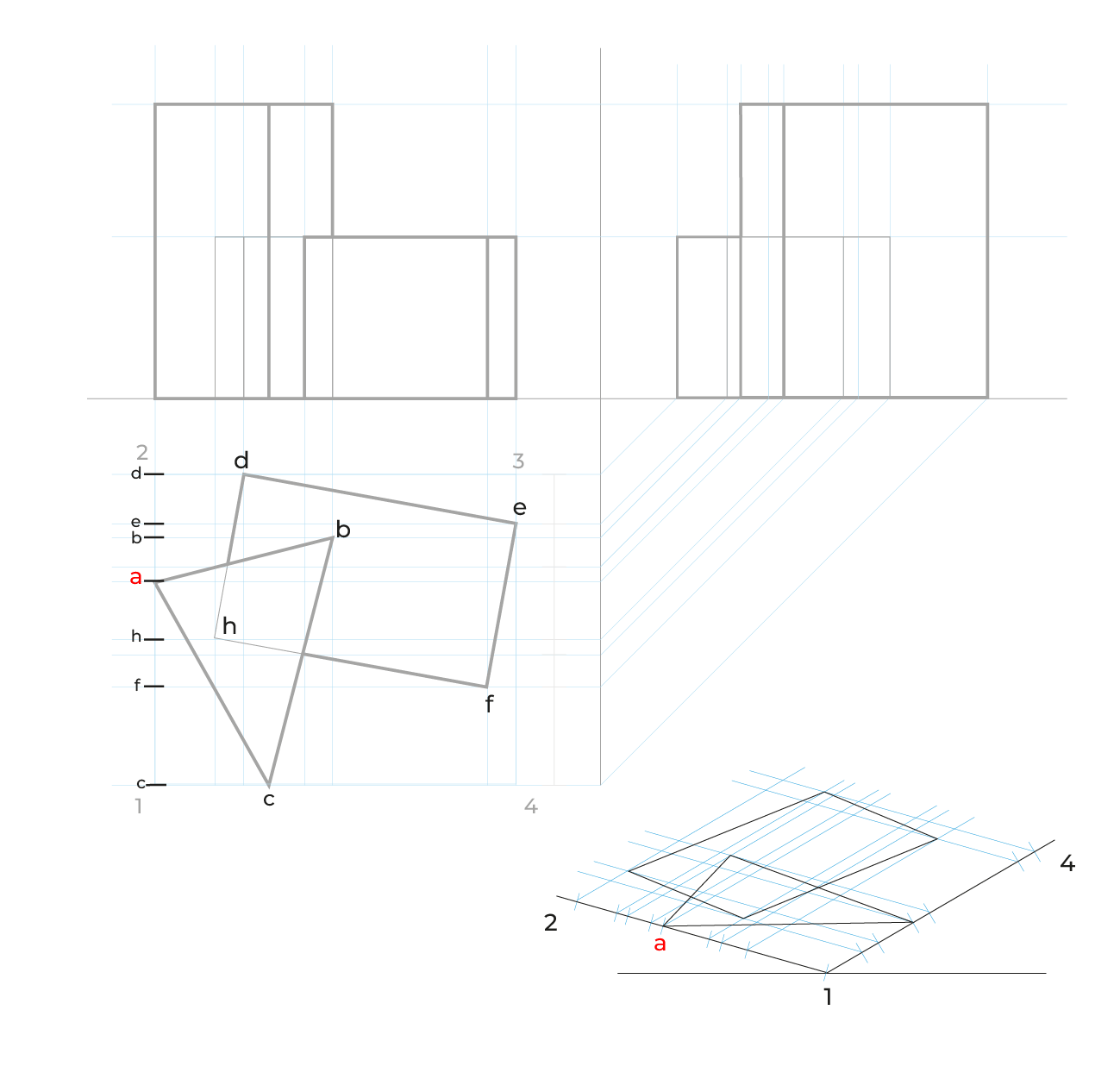
Ángulos empleados para la construcción del subsistema trimétrico

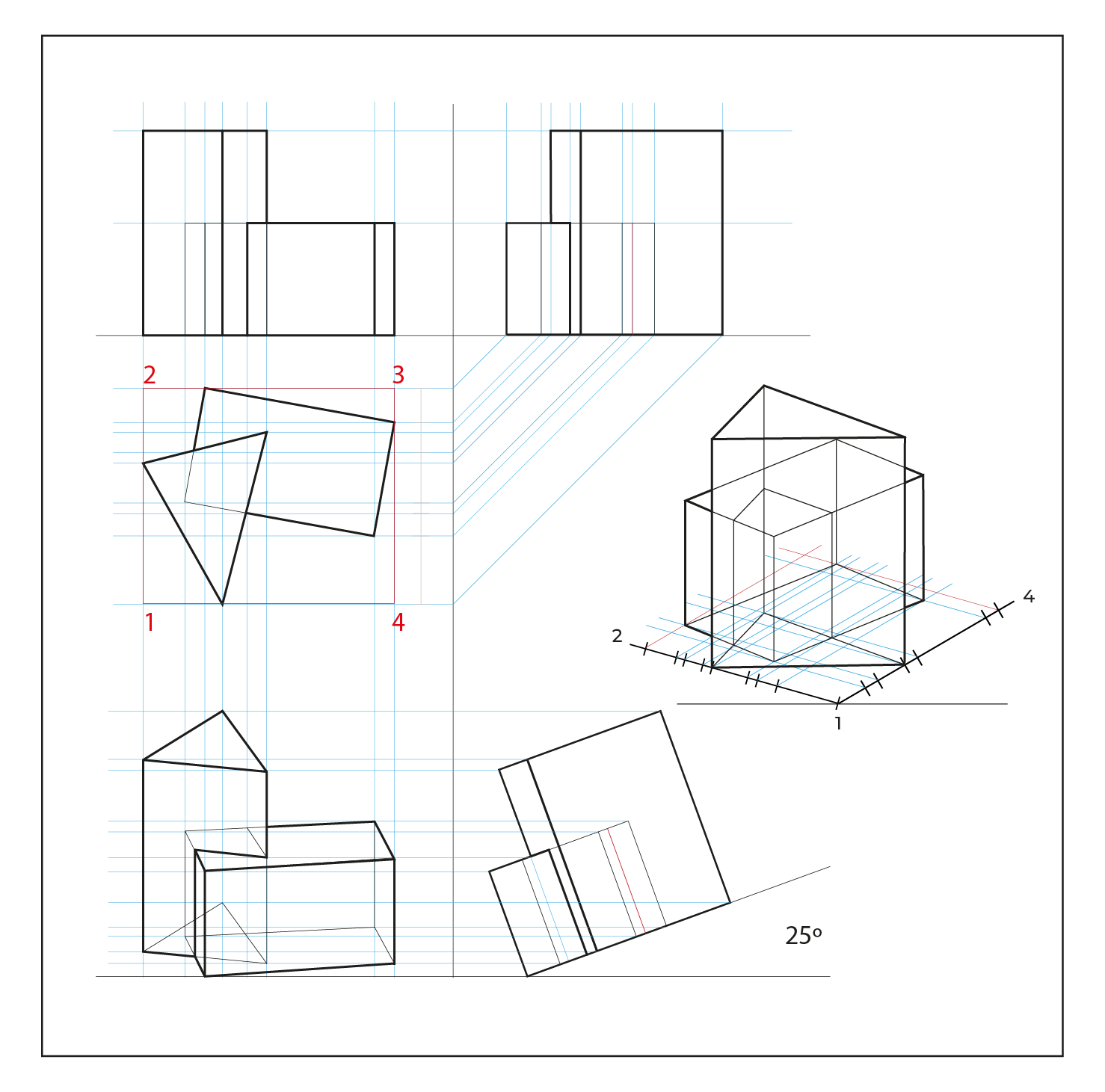
Método por proyección

Consideraciones:

Montea triplanar
Vista superior no alineada a ninguno de los ejes, tampoco girarla a 45º, porque probablemente se alinean varios puntos.
La información se proyecta,lo que aparece en la parte posterior de en la vista superior quedará enfrente, considerar esto para cortes y elementos que se quieran apreciar.
Este método hace las reducciones automáticamente, por lo que no es necesario hacer el proceso de reducción en anchuras y profundidades.

Paso 1

Se baja cada uno de los puntos de vista superior perpendiculares a la línea de tierra (LT), como lluvia de información en la parte inferior

Paso 2

Considerando aproximadamente la altura del objeto, hay que colocar una Línea del Plano del Cuadro (LPC) paralela a la LT.

Paso 3

Colocar un punto, a partir de él se traza una línea con el transportador a 25°.

Paso 4

Sobre la línea diagonal anterior se coloca la información de la vista auxiliar izquierda, se puede pasar toda la vista (líneas y puntos) o solo la información (puntos).

Paso 5

Conectar cada uno de los puntos de la vista auxiliar con las líneas que caen como lluvia de información, en este caso se une punto a que viene dese la vista superior con el punto a que viene desde la vista auxiliar.

Paso 6

El procedimiento se repite, se intersecta la información de los puntos, hasta localizar todos.

Paso 7

Unir la figura y dar calidad de línea, sólo tratando de manera fuerte las aristas que se ven del objeto.

A continuación puedes revisar el siguiente video, en él se explica y se realiza el método desglosado anteriormente, si lo deseas, también descargar los pasos anteriores del apunte PDF Trímétrico método por proyección.

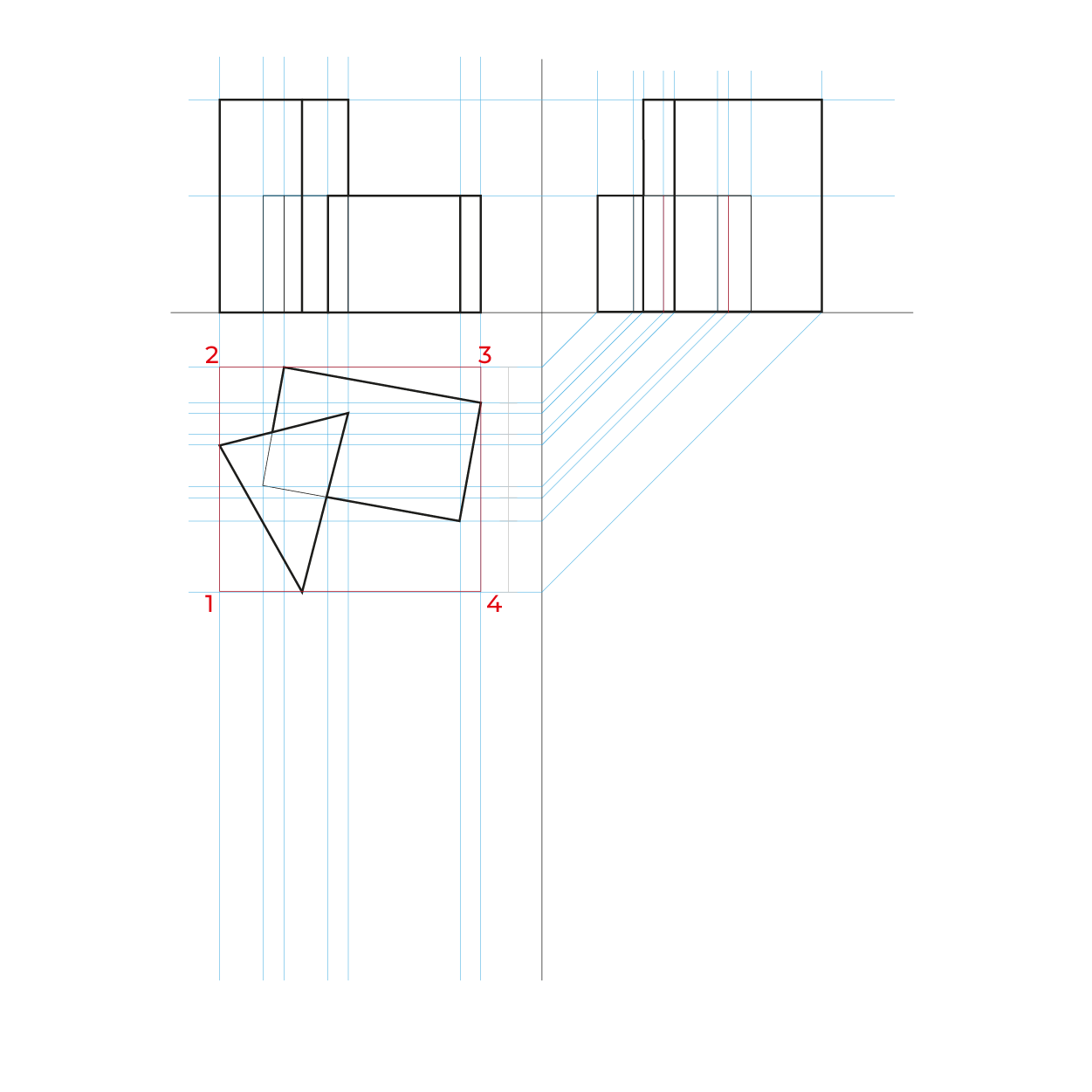
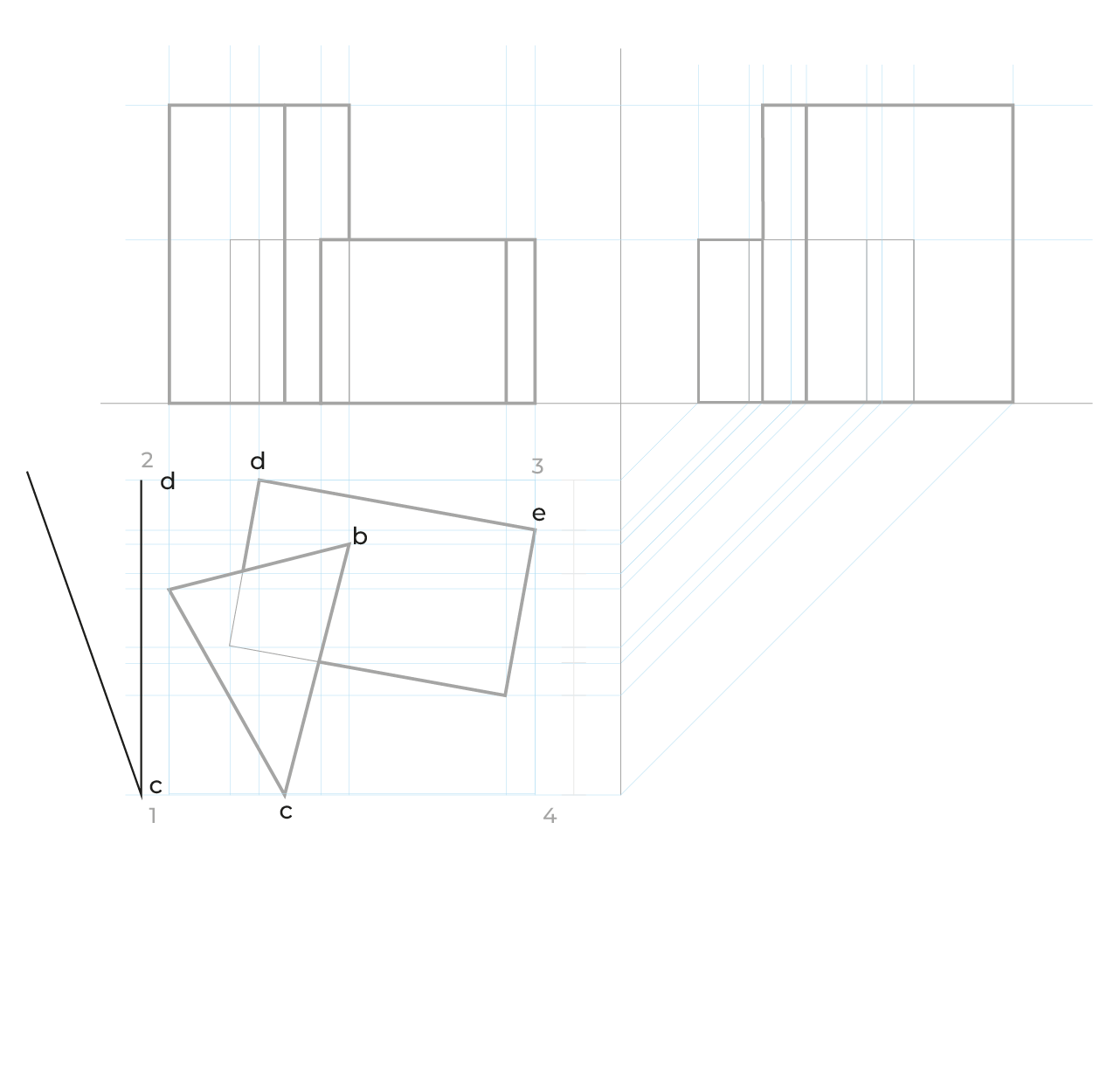
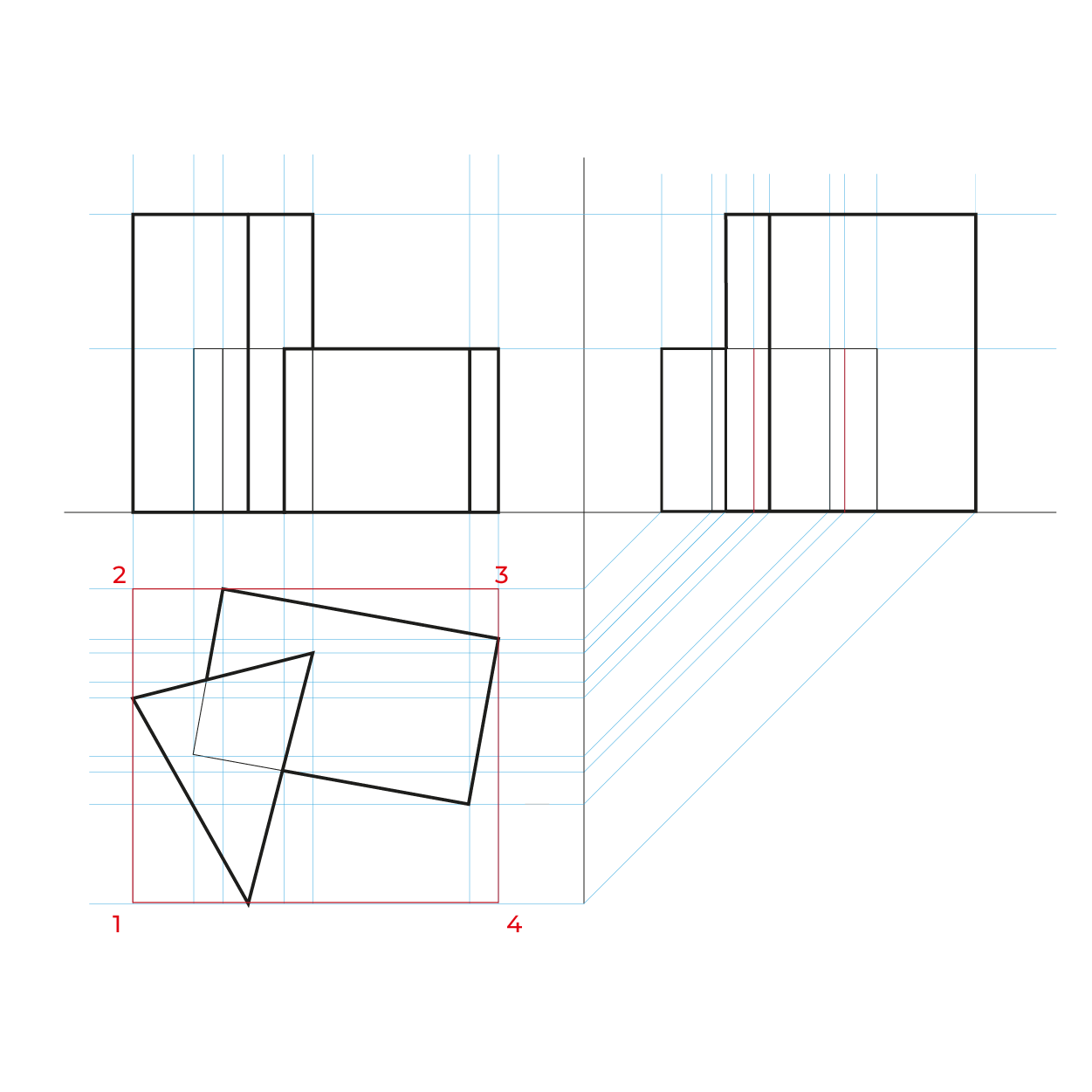
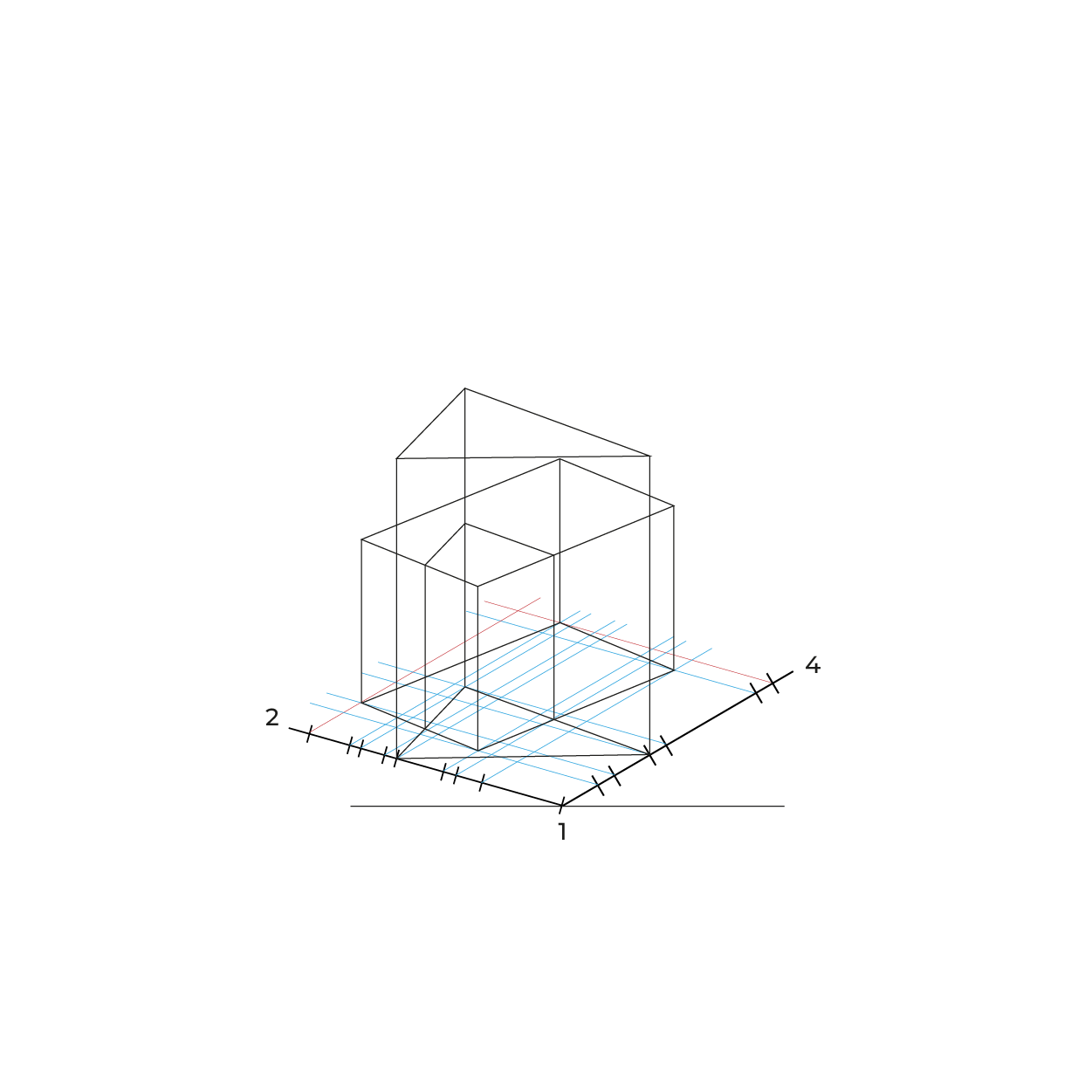
Método por coordenadas

Consideraciones:

Montea biplanar, no es necesaria la vista auxiliar
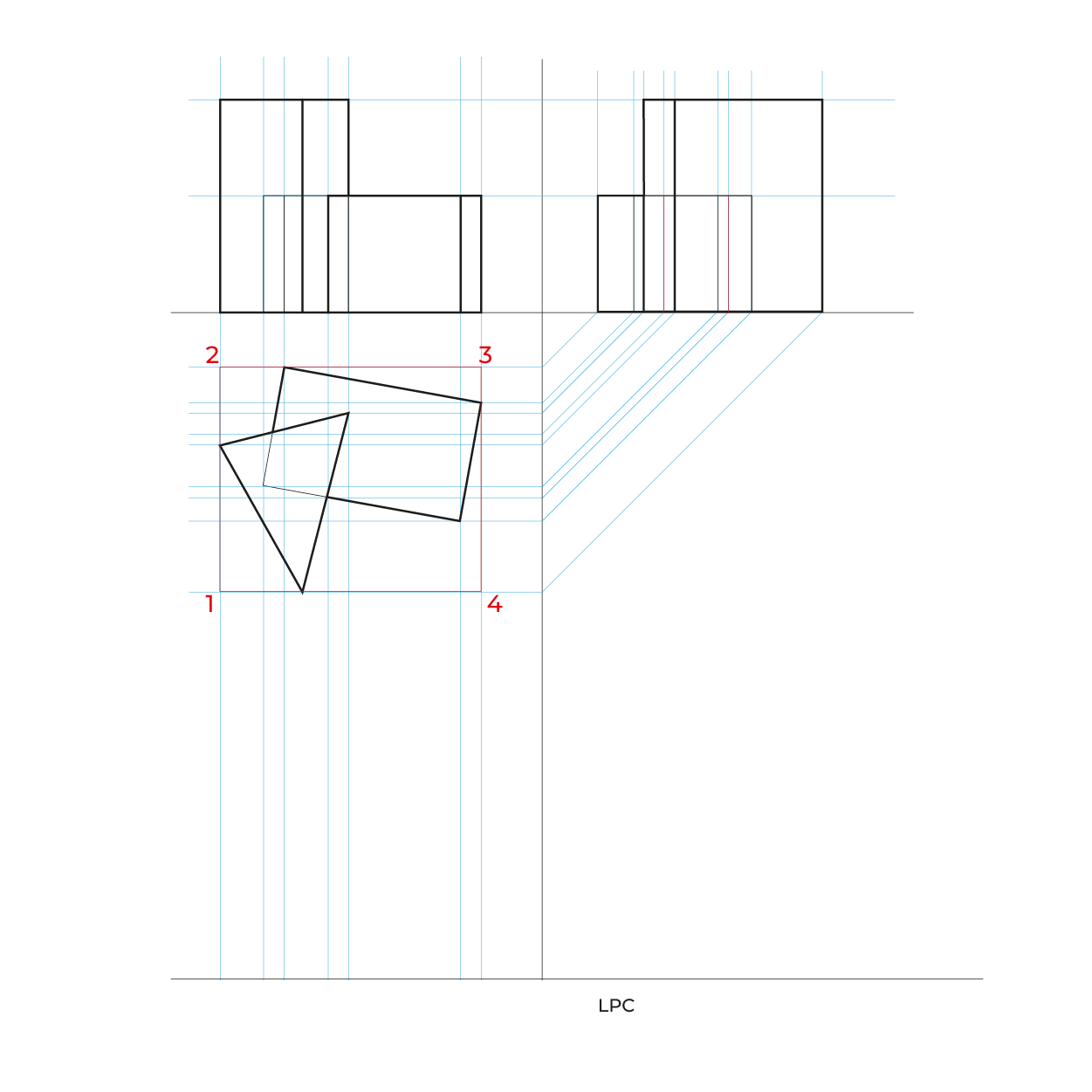
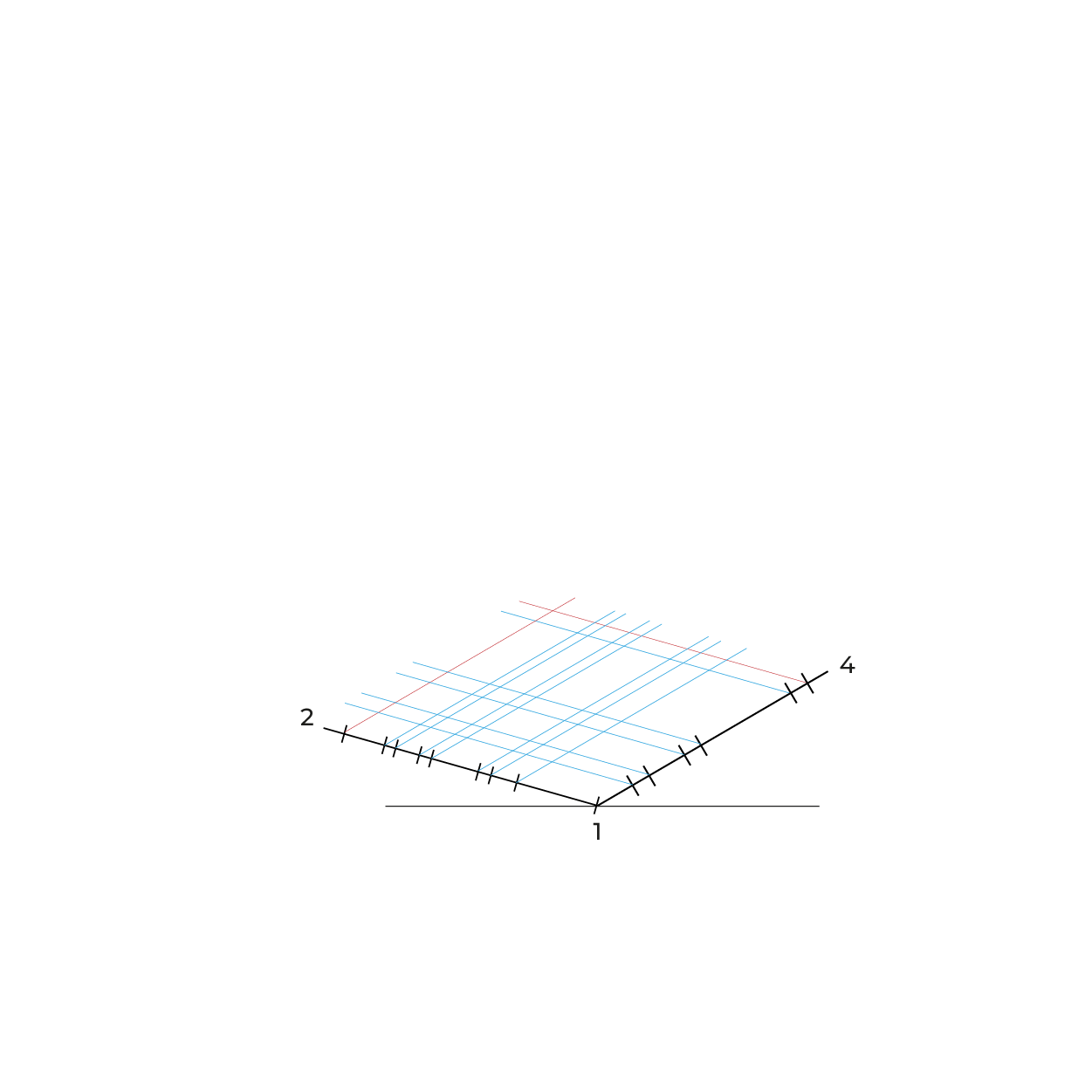
Para facilitar la construcción del subsistema no utilizaremos el triedro, construiremos un plano geometral a partir de la línea del plano del cuadro (LPC).
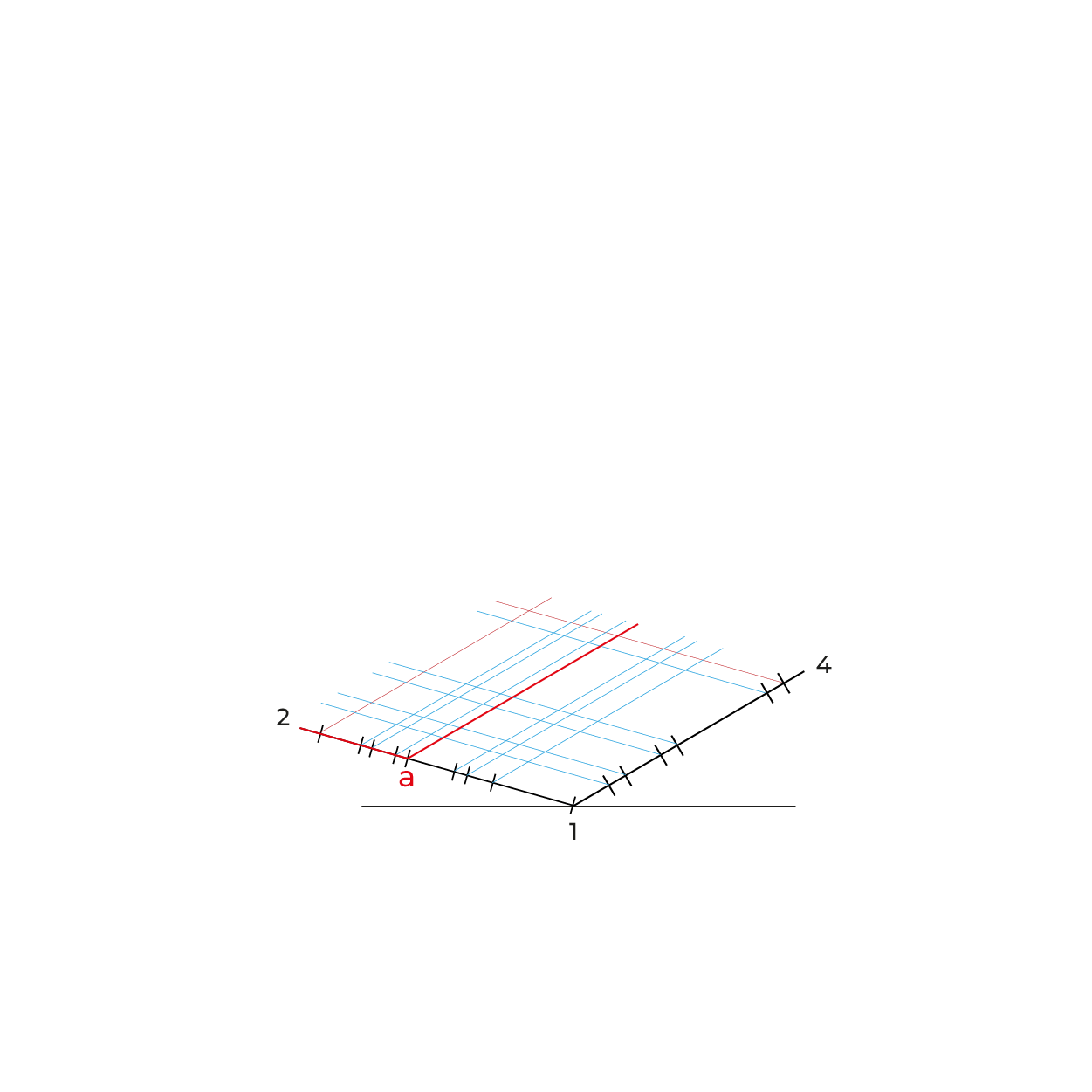
De preferencia realizar un semi-encaje en la vista superior considerando los puntos extremos, esto nos permitirá vaciar de manera correcta la información, sin equivocaciones.
En este método es necesario hacer el proceso de reducción en anchuras y profundidades.

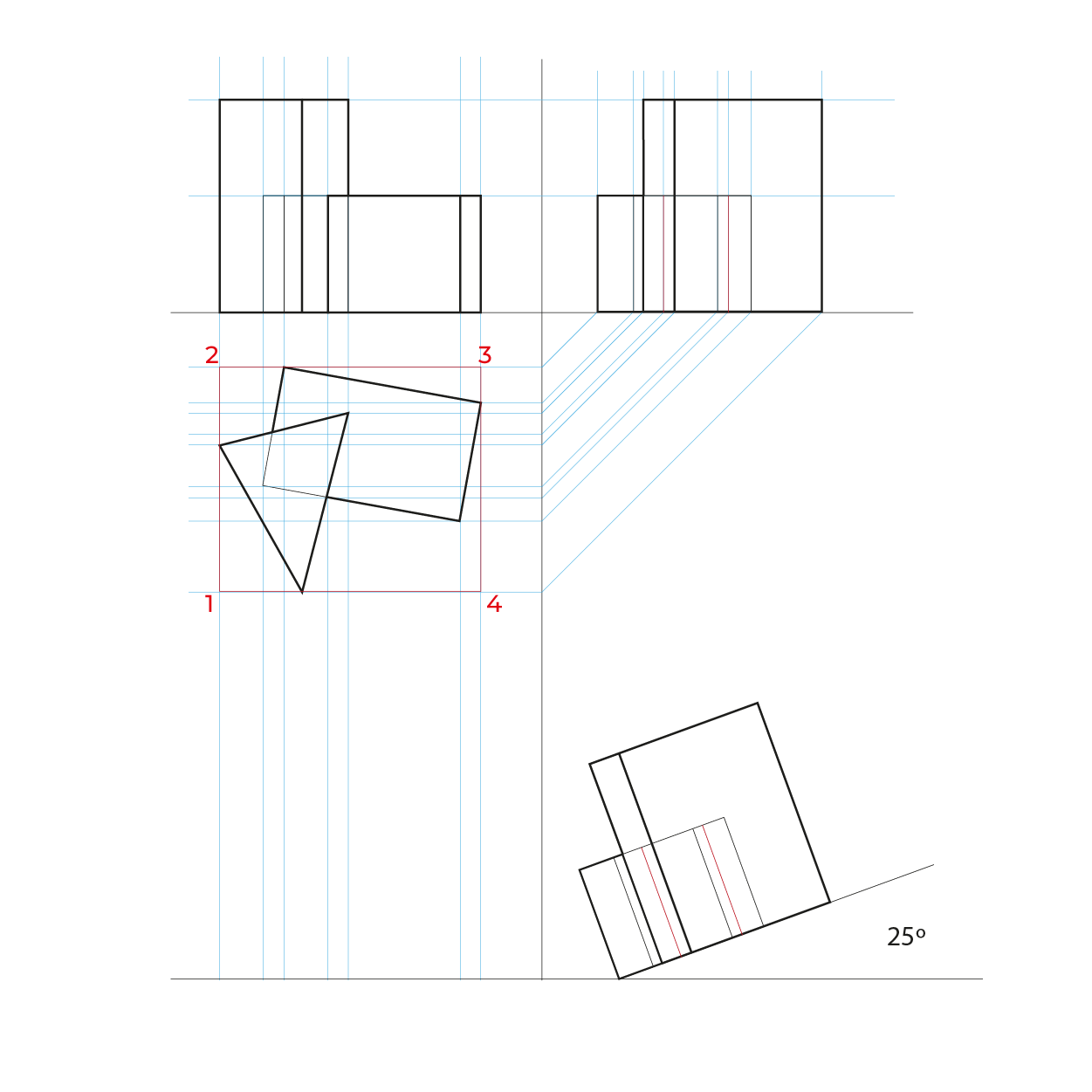
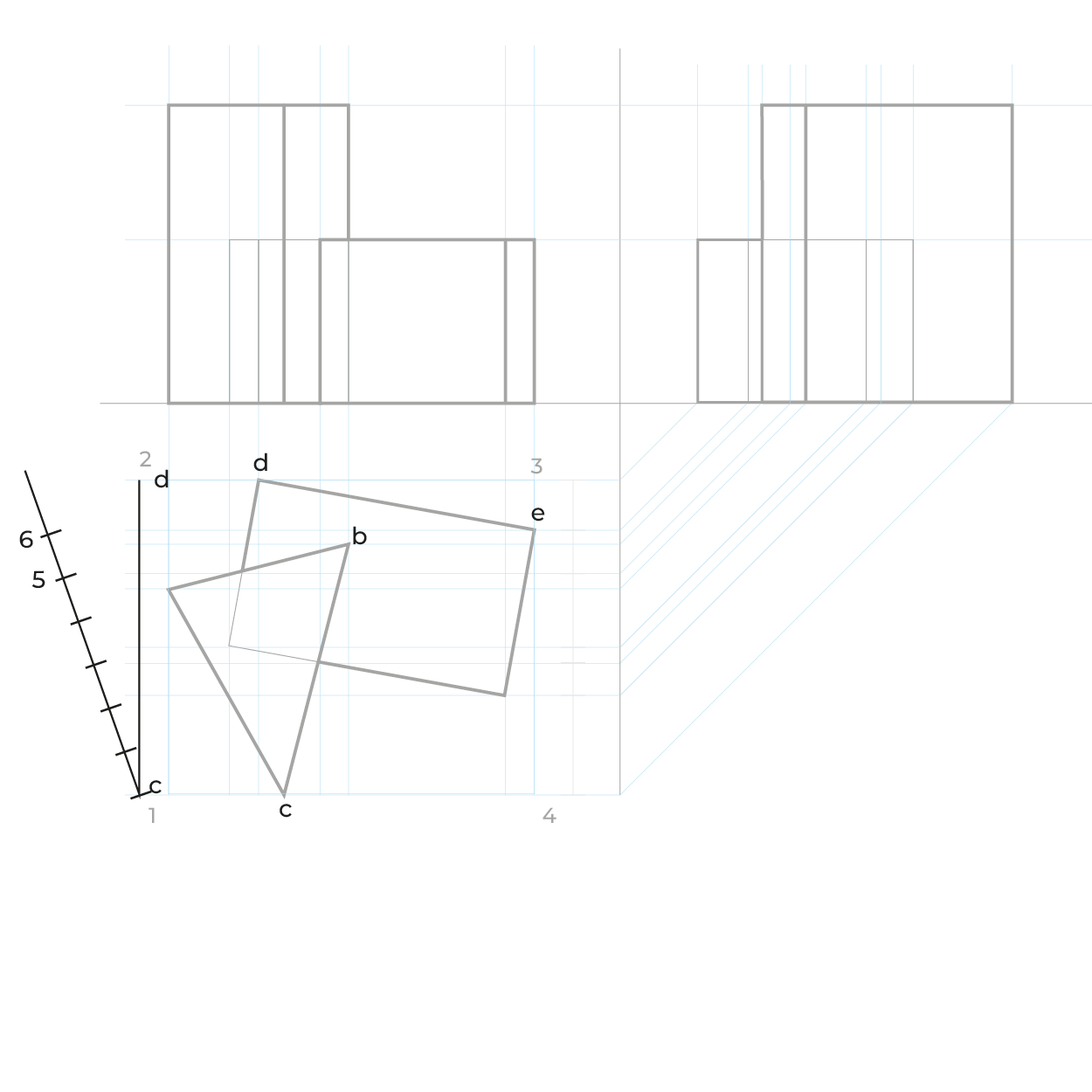
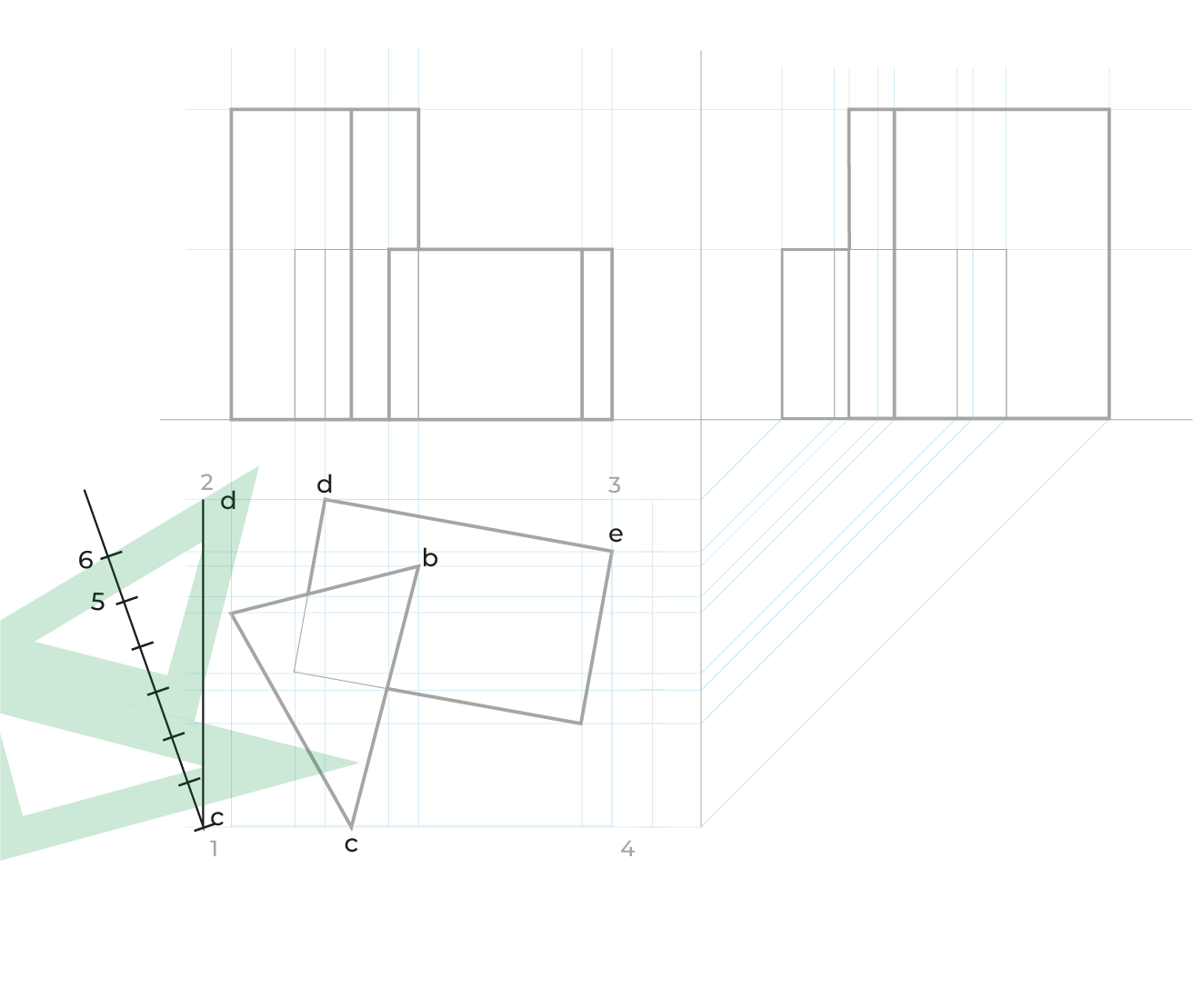
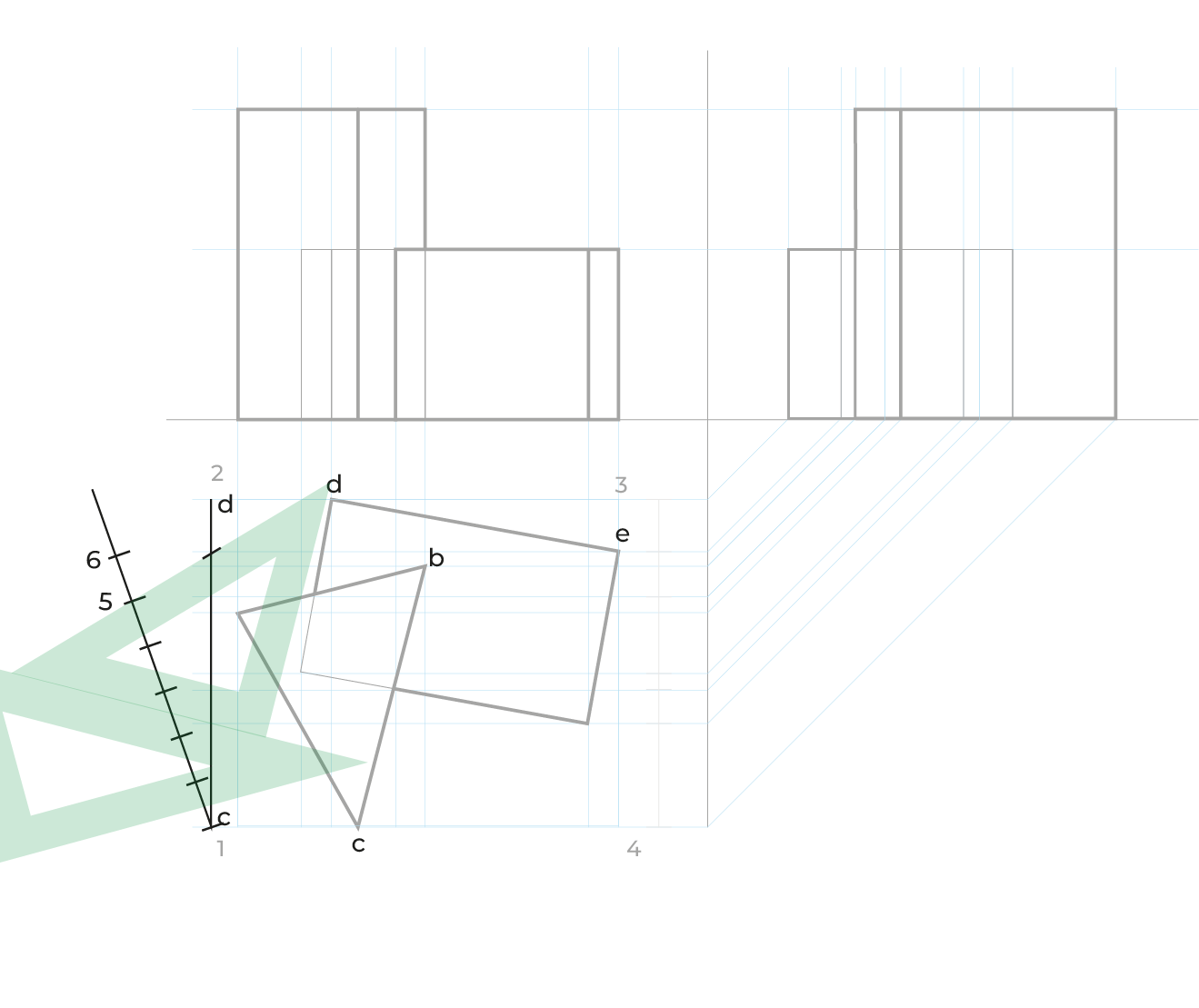
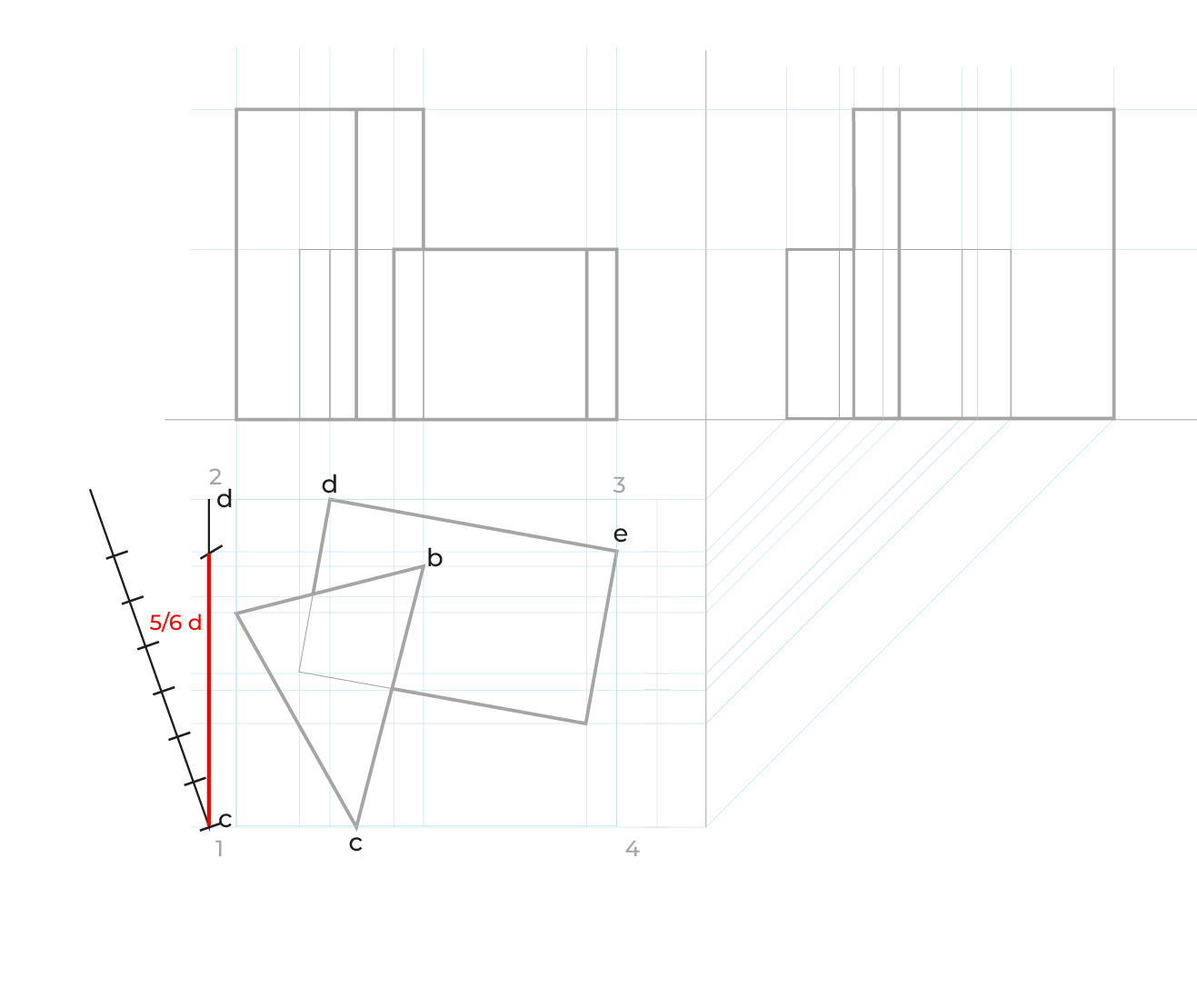
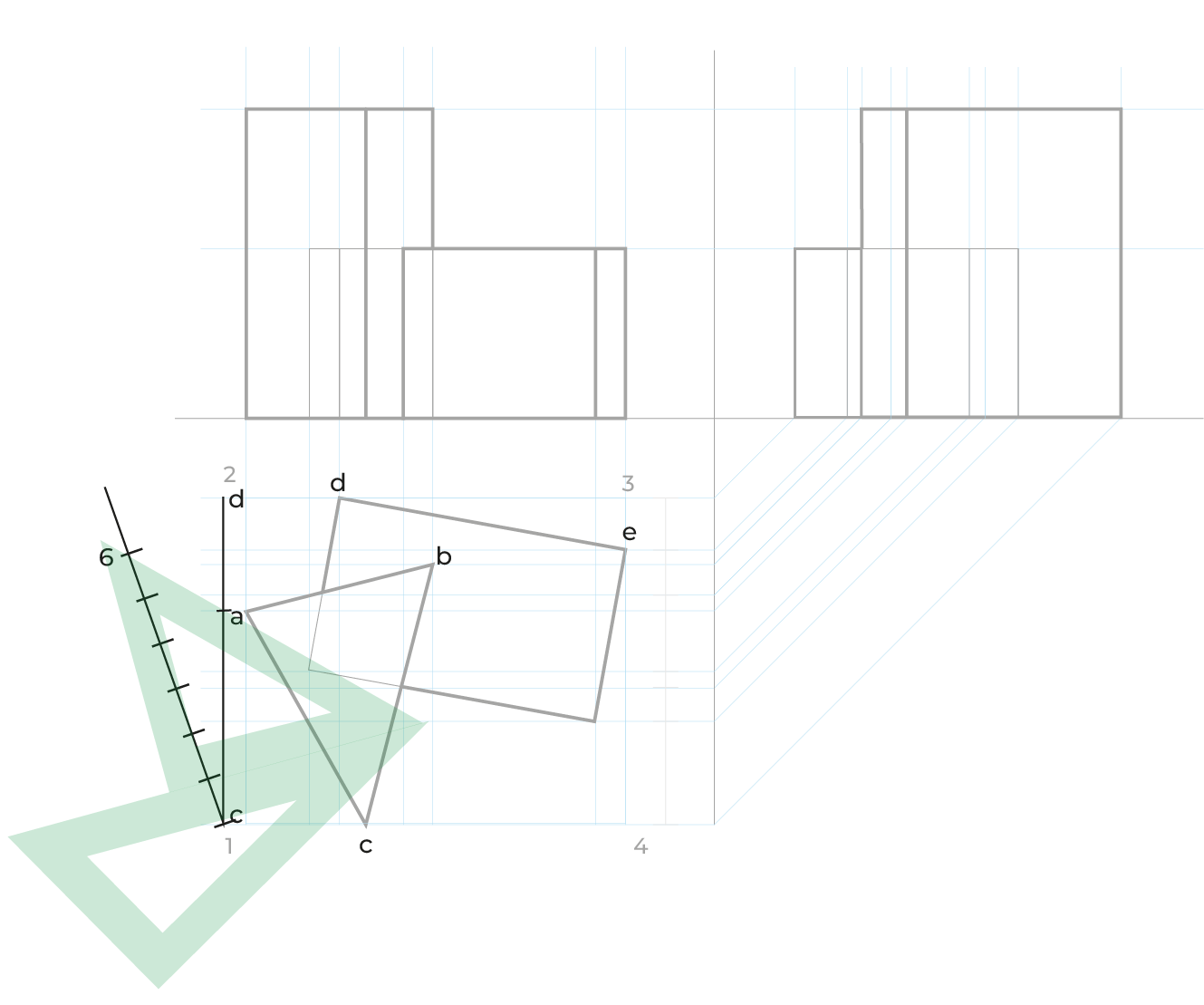
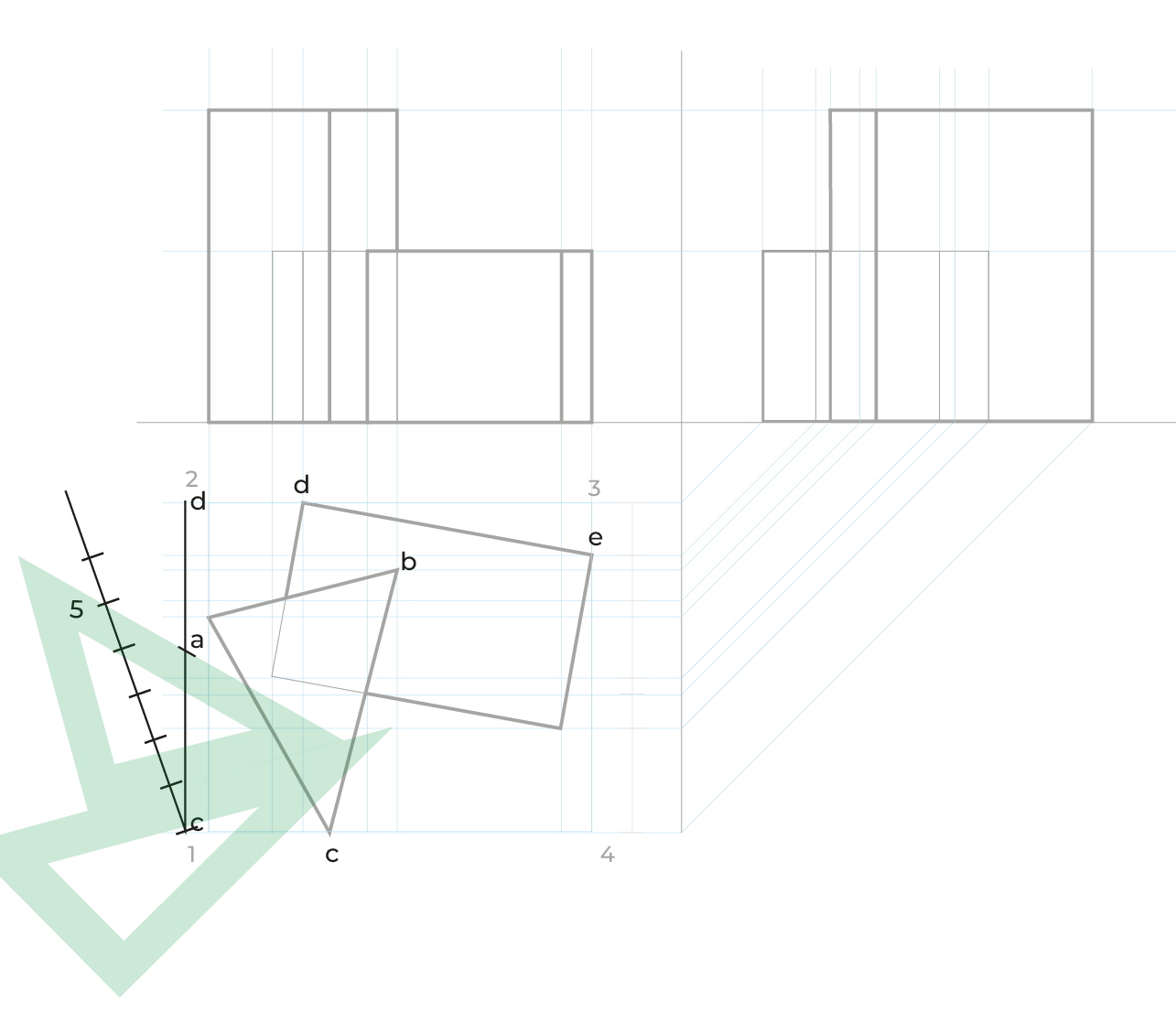
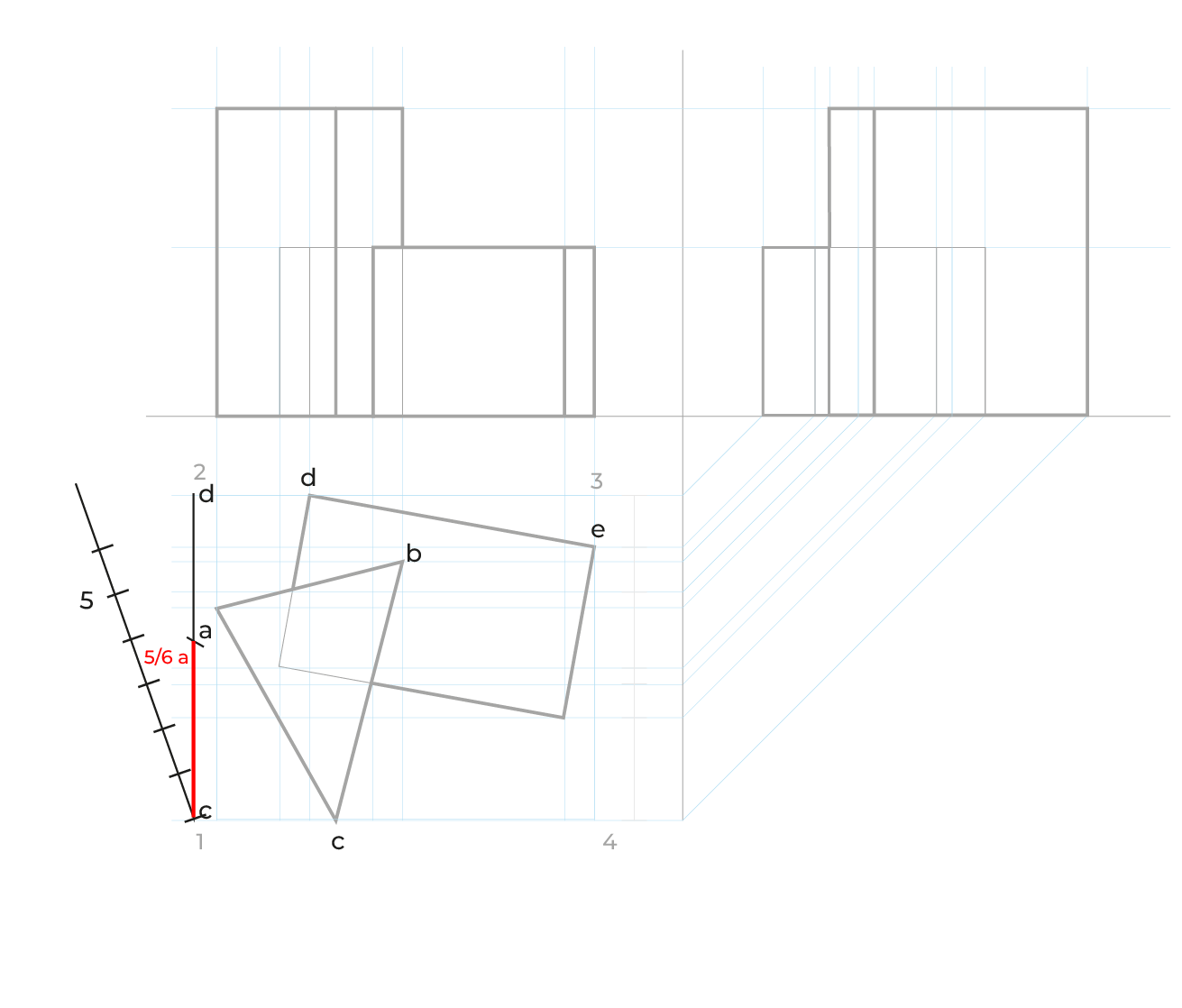
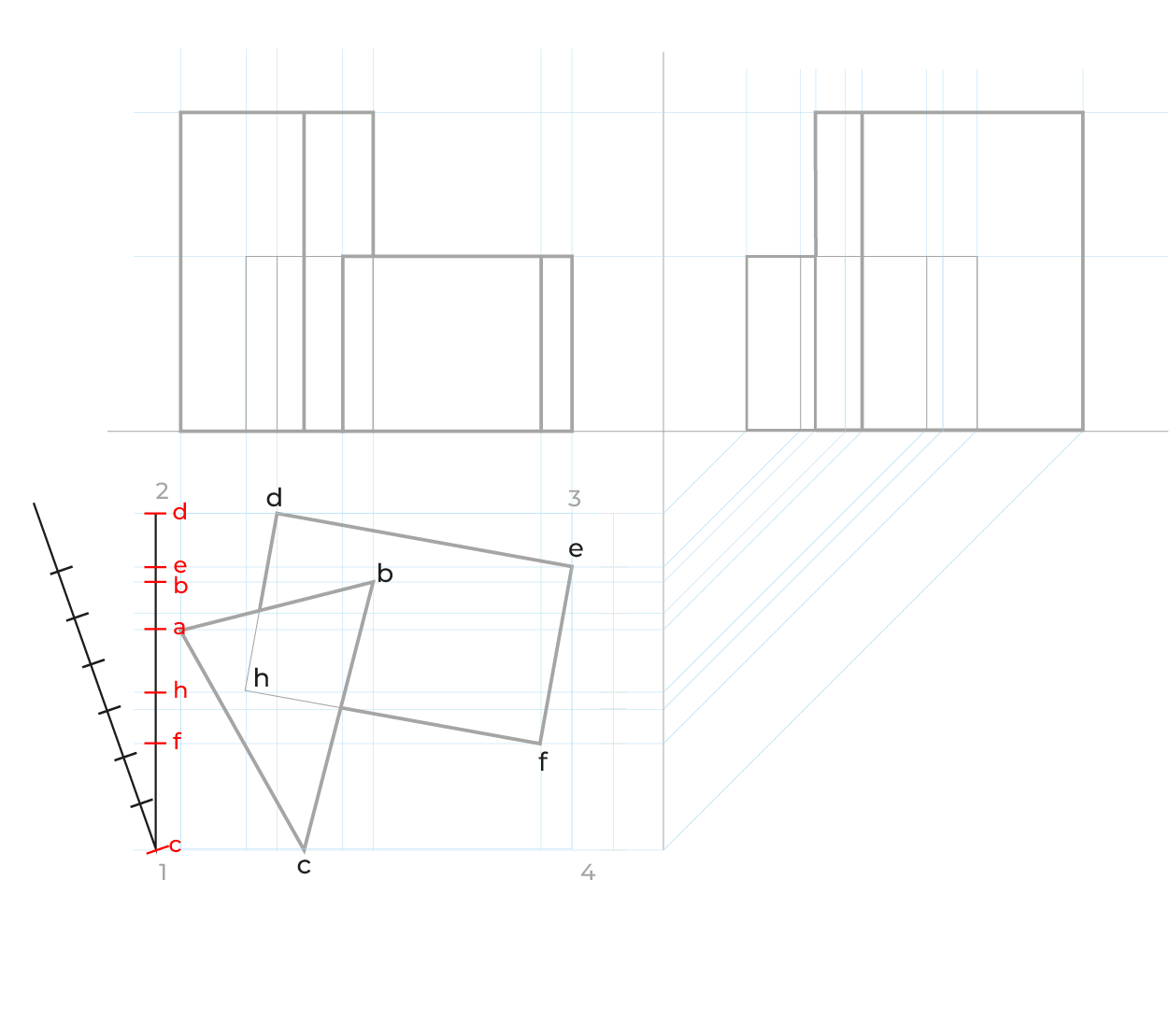
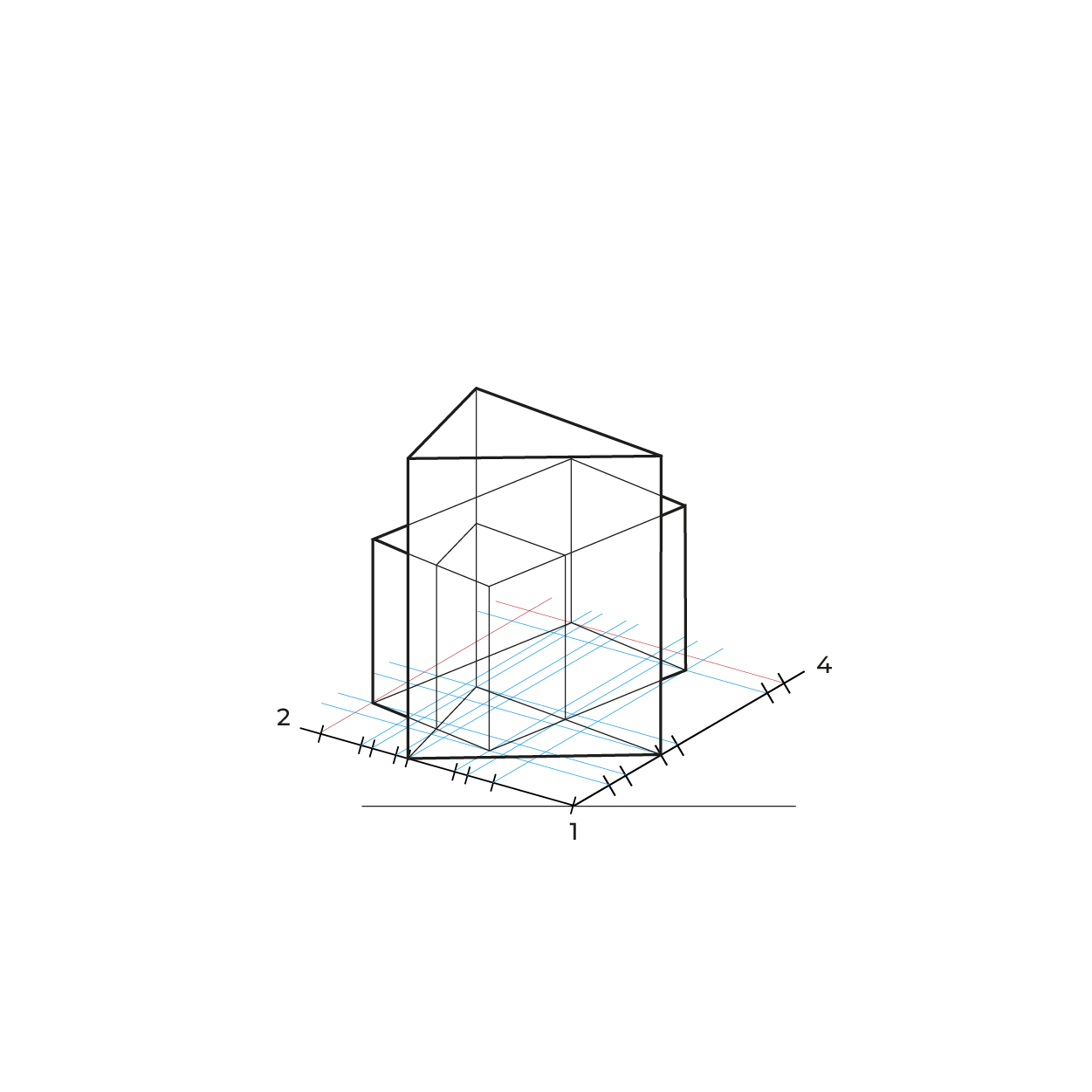
Reducciones

El método es idéntico al utilizado en el subsistema dimétrico, las anchuras las reduciremos de la misma manera, en el ejemplo siguiente sólo ejemplificamos las reducciones en anchuras, pero este método requiere las reducciones en ambos.

Paso 1

Trazamos una línea a los grados que sean, considerando el punto de origen del segmento que se desea dividir. En este caso el punto c es como origen.

Paso 2

Dividimos la línea en la cantidad deseada, en este caso seis, porque queremos reducir 5/6 las anchuras. No importa la dimensión de estas divisiones, sólo que sean de tamaños iguales.

Paso 3

Con nuestras escuadras trazamos una línea del punto extremo del segmento a reducir al segmento 6, en este caso el punto d.

Paso 4

Sin mover la escuadra de apoyo, deslizamos la otra escuadra al segmento 5, y trazamos una línea paralela que cortara de nuevo el segmento a dividir.

Paso 5

Donde se genera este corte, es el extremo de nuestra magnitud reducida, en este caso 5/6 partes del segmento c - d.

Paso 6

Con nuestras escuadras trazamos una línea de uno de los puntos a reducir al segmento 6, ahora el punto a.

Paso 7

Sin mover la escuadra de apoyo, deslizamos la otra escuadra al segmento 5, y trazamos una línea paralela que cortará de nuevo el segmento a dividir.

Paso 8

Donde se genera este corte, es el extremo de nuestra magnitud reducida, en este caso 2/3 partes del segmento c - a.

Paso 9

Este procedimiento se repite con cada uno de los puntos en anchura de nuestra figura.

Paso 10

En caso del punto c al ocuparlo como origen no es necesario hacer ninguna reducción, se pasa como origen al plano geometral de nuestra construcción.

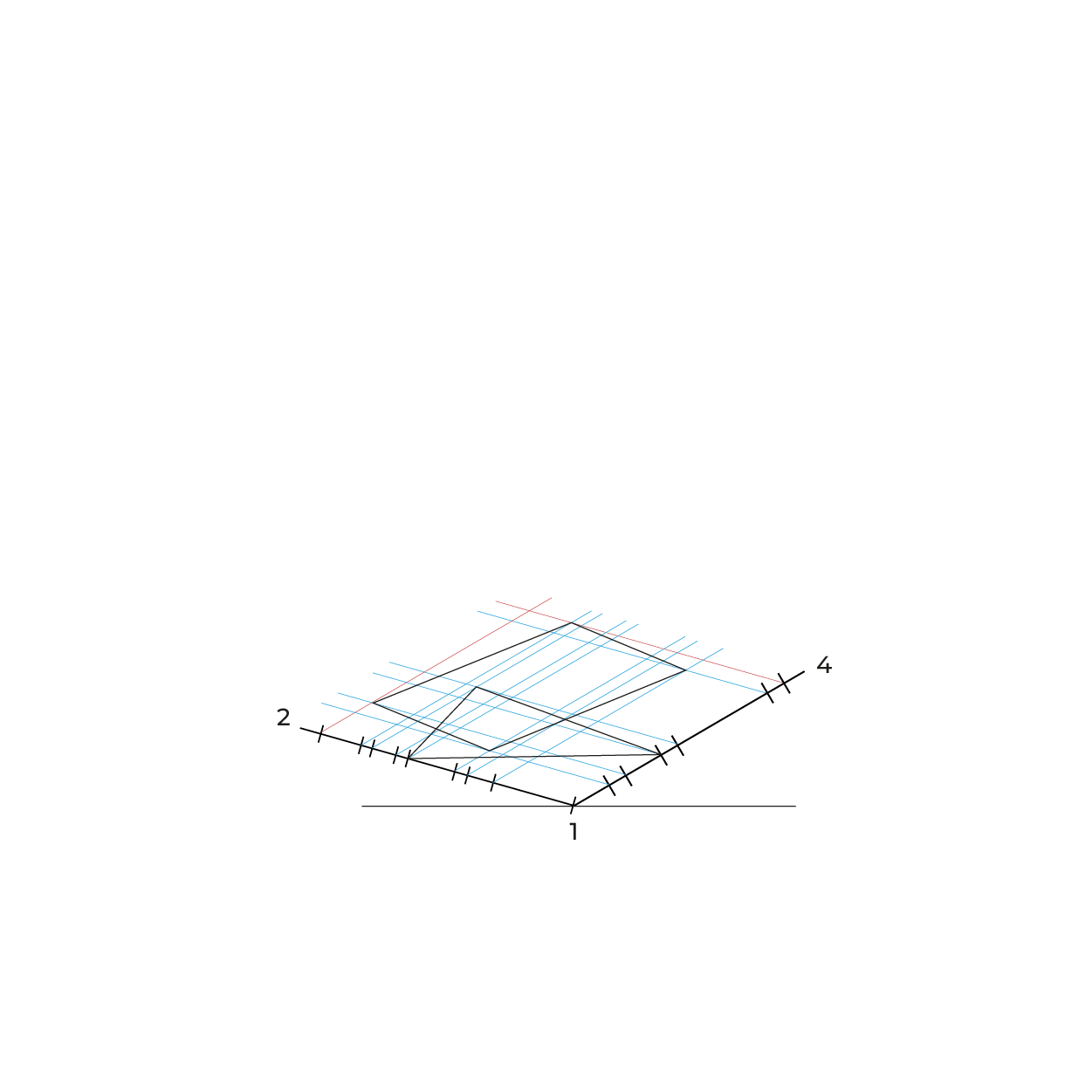
El proceso:

Paso 1

De preferencia trazar un semiencage con los puntos extremos, numerando de esta forma (al igual que en todos los métodos de coordenadas) y realizar las reducciones en profundidad a 2/3 y en anchuras a 5/6.

Paso 2

Se coloca una pequeña LPC y a partir de ella se genera un plano geometral de 135°, se construye a partir de un eje de anchuras con una inclinación de 15° y un eje de profundidades de 30°.

Paso 3

Vaciamos la información de profundidades, de 1 a 2 y de anchuras, de 1 a 4 .

Paso 4

Con líneas paralelas y perpendiculares a los ejes unimos 2 y 4, esto nos delimitará el espacio a utilizar. Ninguno de los puntos de nuestra figura deberá salir de este espacio.

Paso 5

A partir de los puntos en anchuras trazar líneas guía paralelas al eje contrario, del lado contrario hacer lo mismo, a partir de los puntos en profundidades trazar líneas guía paralelas al eje contrario.

Paso 6

Localizar por coordenadas la intersección de los puntos, en este caso el punto a.

Paso 7

Ubicar sobre el piso cada uno de los puntos que corresponden al objeto a construir

Paso 8

Levantar los puntos que tengan altura por medio de líneas verticales, perpendiculares a la LPC (no a alguno de los ejes) y colocar la altura correspondiente a la montea.