 Apuntes de diseño
Apuntes de diseño
Subsistema dimétrico
Soledad Ortiz | Uriel FlamencoLab. taller en diseño en iconicidad y entornos I
 Apuntes de diseño
Apuntes de diseño
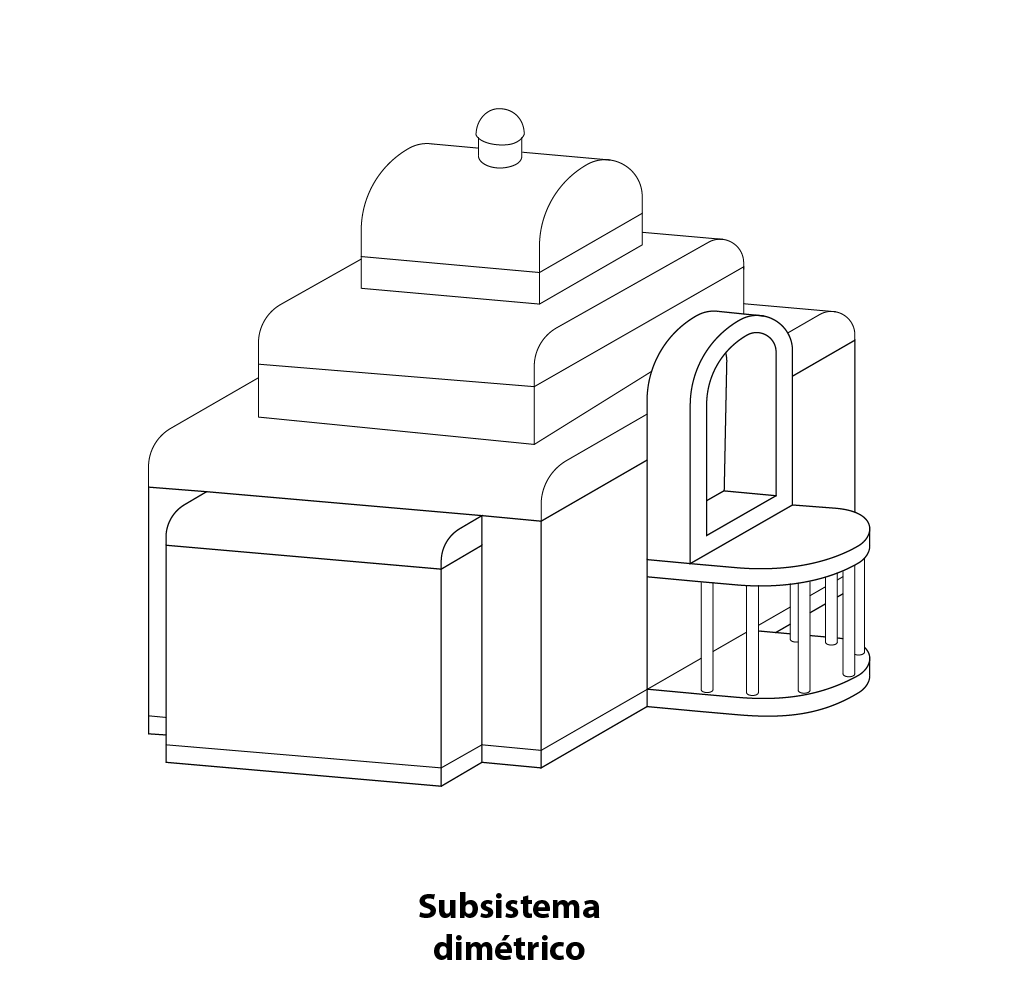
La palabra dimético proviene de grigo “dis” que significa ”dos” y “metron” que significa “medida”. Una representación de tipo dimétrico consiste en la representación gráfica de un objeto tridimensional de manera bidimensional, en la cual, los tres ejes que constituyen el plano de proyección forman dos ángulos de igual amplitud y un ángulo de amplitud diferente.
En éste tipo de subsistema, las dimensiones correspondientes a cada uno de los ejes se manejan en dos escalas, es decir, existe alteración en las medidas del plano descriptivo (montea) correspondientes a las profundidades, con lo que ocurre una ligera deformación en la vista del objeto, misma que refleja una disminución aparente en su tamaño, la cual resulta proporcional a la distancia que se percibe por el ojo del humano.
El ajuste a las profundidades se hace a ⅔ de la magnitud real del objeto en la montea.
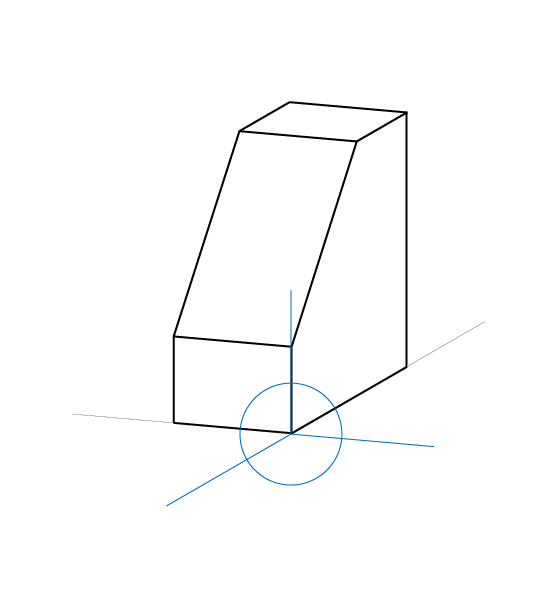
Los tres ejes que constituyen el plano de proyección forman dos ángulos de igual amplitud y un ángulo de amplitud diferente.
Compensación en las magnitudes:
Las profundidades se reducen a 2/3 partes. 1:1:2/3
No se puede hacer la construcción con los ángulos usualmente utilizados en dibujo lineal.
Apta para representar objetos con una anchura predominante.
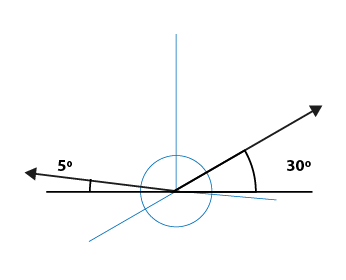
Ángulos que utilizaremos para construcción del plano geometral
Este método nos ayudará a generar divisiones geométricamente de un segmento sin necesidad de recurrir a instrumentos matemáticos, la famosa calculadora. Permitirá tener mayor precisión y no tener que recurrir a precisiones milimétricas con el uso de la regla.
Nota: es recomendable no llevar todas las líneas a los segmentos, solo basta con cortar las líneas y de preferencia reducir uno de los puntos y trasladarlo al plano geometral y así sucesivamente, esto permitirá tener menos confusión de cuales son las anchuras y las anchuras reducidas.
También pueden trazar esto sobre un albanene para dejar libre la montea.

Ejemplo de lámina del subsistema dimétrico por método de proyección y coordenadas
Puedes descargar los pasos anteriores en un apunte PDF Dimétrico método por coordenadas.
Ramos García, F. (1976). Prácticas de dibujo arquitectónico. Barcelona: Gustavo Gili.
Reiner Thomae. (1978). Perspectiva y axonometría. México: Gustavo Gili.
Ortiz, M. (2020). Subsistema dimétrico, método por coordenadas. [archivo de video]. Consultado de https://youtu.be/3BHkXiRAIm8